bobby2k
- 126
- 2
Take a look at this theorem.
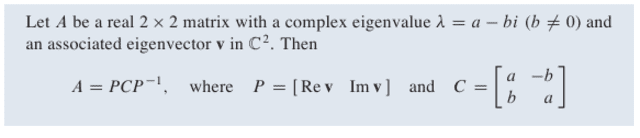
Is it a way to show this theorem? I would like to show it using the standard way of diagonalizing a matrix.
I mean if P = [v1 v2] and D =
[lambda1 0
0 lambda D]
We have that AP = PD even for complex eigenvectors and eigenvalues.
But the P matrix in this theorem is real, and so is the C matrix. I think they have used that v1 and v2 are conjugates, and so is lambda 1 and lambda 2.
How would you show this theorem? Can you use ordinary diagonolisation to show it?
Is it a way to show this theorem? I would like to show it using the standard way of diagonalizing a matrix.
I mean if P = [v1 v2] and D =
[lambda1 0
0 lambda D]
We have that AP = PD even for complex eigenvectors and eigenvalues.
But the P matrix in this theorem is real, and so is the C matrix. I think they have used that v1 and v2 are conjugates, and so is lambda 1 and lambda 2.
How would you show this theorem? Can you use ordinary diagonolisation to show it?
Last edited: