Interference Pattern versus SR

[Adel Makram]

I posted this thought experiment in a previous thread before 4 months or so, but I would like to reiterate it now:
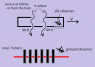
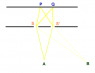
A frame of reference (FOR) has double slits moves relative to a ground FOR. Let`s make an arrangement so that when the 2 ends of FORs coincide, 2 small slits of moving FOR are opened at the same time relative to the ground observer for a brief moment to allow just 2 photons to enter from an electromagnetic source put on the opposite side of him. Let `s make the distance between the 2 slit small enough comparable to the wave-length of the photons to cause an interference pattern.
For the ground observer, he sees 2 slits open at the same time and therefore the 2 photons entering the 2 slits and create an interference pattern on a screen on his frame.
But according to SR interpretation, the moving FOR`s observer sees the front slit opens for a brief moment and then shuts before the rear one opens,,, so at one time, only one slit opens and therefore no interference pattern could ever occur. But when he looks at the screen from his window, he will see an interference pattern on the ground screen.
Can the train observer now explain why this interference pattern occurs when just the slits open one at a time?

 

[Mentz114]

Nothing strange will be observed because interference depends on phase, which is a scalar and therefore Lorentz invariant. Both observers will see the same pattern ( or non-pattern ).

 

[Adel Makram]

Nothing strange will be observed because interference depends on phase, which is a scalar and therefore Lorentz invariant. Both observers will see the same pattern ( or non-pattern ).

How will the moving FOR see the same pattern as the ground one! the idea is the interference pattern will not happen unless the 2 slits open at the same time. If this the case for the ground one, it will not be the case for the moving one, so he will not see the pattern. The moving FOR will document the near slit open and shut before the rear one, so at any time only one slit open and no interference pattern occurs !

 

[Mentz114]

Relative simultaneity. If two events are at the same time in one frame they are not necessarily simultaneous in another.

Interference patterns are cause by the coming together of worldlines, and so are made up of events. The existence of an event cannot be altered by a Lorentz transformation.

 

[Adel Makram]

Relative simultaneity. If two events are at the same time in one frame they are not necessarily simultaneous in another.

Interference patterns are cause by the coming together of worldlines, and so are made up of events. The existence of an event cannot be altered by a Lorentz transformation.

but the sequence of events can! at least according to SR. if 2 slits open simultaneously according to ground observer, they will not according to the slits observer

 

[Mentz114]

but the sequence of events can! at least according to SR. if 2 slits open simultaneously according to ground observer, they will not according to the slits observer

Your point being ? You've just restated my first sentence. It is not possible to construct a causal paradox based on inteferference for the reasons given. If you think you have, you've made a mistake.

 

[Adel Makram]

if the 2 slits open one at a time relative to slit`s FOR, the slit observer will not see the interference pattern from his window. There will not be even a wave-phase to talk about! MY question, how the physical reality, the interference pattern, can be matter of conflict between the 2 observers?

 

[Adel Makram]

Y It is not possible to construct a causal paradox based on inteferference for the reasons given. If you think you have, you've made a mistake.

I think it is possible to create a paradox based on my experiment,,,

 

[Mentz114]

if the 2 slits open one at a time relative to slit`s FOR, the slit observer will not see the interference pattern from his window. There will not be even a wave-phase to talk about! MY question, how the physical reality, the interference pattern, can be matter of conflict between the 2 observers?

There won't be any conflict between the observers.

Certainly if the slits and the screen are oriented at right angles to the direction of relative motion, there will be no relativistic effects.

 

[Adel Makram]

the period of opening of slits can be chosen arbitrarily so as to make the front slit opens and closed before the back slit open relative to the slit observer. But for the ground observer, they are opened at the same time

 

[Doc Al]

the period of opening of slits can be chosen arbitrarily so as to make the front slit opens and closed before the back slit open relative to the slit observer. But for the ground observer, they are opened at the same time

What matters is not whether the slits are open at the same time or not, but whether the light from each slit reaches the same spot on the screen at the same time. All observers must agree on that.

 

[Mentz114]

the period of opening of slits can be chosen arbitrarily so as to make the front slit opens and closed before the back slit open relative to the slit observer. But for the ground observer, they are opened at the same time

Please draw a diagram of the setup and someone will show you why there's no paradox or conflict.

 

[Adel Makram]

What matters is not whether the slits are open at the same time or not, but whether the light from each slit reaches the same spot on the screen at the same time. All observers must agree on that.

They will reach at the same time, that is why there is an interference pattern, which I am not in doubt for. But, according to the quantum M interpretation, it is just a single slit experiment for the slit observer

 

[Adel Makram]

for a slit observer, if there is some way to label which slit the photon enters, then no interference pattern will form

 

[bahamagreen]

I like this thought problem. Let's see if we can find the problem (the incorrect assumptions) by breaking down the question some more...

The way it is presented is that the stationary FOR observes photons going through both slits together and sees an interference pattern; then the question is if the moving FOR would observe that pattern after seeing the photons pass through single slits in sequence.

Since no objection has been made to the problem, may we assume that the assumptions there are correct - that the stationary observer will see photons go through two slits and make a pattern, and the moving FOR will see photons go through single slits?

One assumption is that a FOR should expect to see a pattern if the observation is that the photons go through two slits at the same time. Is this correct? Is this not the result of experiments to examine this very thing?

Another assumption is that the relative motion of a FOR does not impact the result... all FOR will see a pattern if they see the two photons go through two slits at the same time. Is this correct? Is this not what SR expects?

Another assumption is that a FOR should not expect to see the pattern is it is observed that the photons go through single slits in sequence. Is this correct? Is this not the observation from experiment?

Another assumption is that the relative motion of the FOR has no effect on observing the lack of pattern if the photons go through single slits in sequence. Is this also not correct?

So the assumptions so far are:
For any FOR one should expect to see a pattern if one observes the photons going through two slits together, and one does not expect to see a pattern if one observes the photons going through single slits in sequence.

The paradox is that the two FOR have opposing observations about whether the two photons go through a pair of slits together or whether they go through single slits in series. The paradox is that these two observations and their resulting expectation for a pattern or not are different... that based on the assumptions above, one will see a pattern and the other will not.

Menzt114 is stating that both will see the same thing (pattern or not pattern), but has not stated which of these is the observed result. Either way maintains the paradox if the above assumptions hold.

The presentation could be made the other way around... it could be stated first that the moving FOR sees the photons pass through single slits in sequence thereby seeing no pattern, but then the paradox is that the stationary FOR will see them go through two slits at the same time and will see a pattern.

Either way, the question is all about how both must see the same thing... and exactly which observation will be that same thing, the pattern or no pattern? And then, why the moving FOR should see sequential photons through single slits make a pattern, or why the stationary FOR should see photons go through two slits together and not see a pattern.

Menzt144, if both must see the same thing (pattern or no pattern), which is it, based on the presentation of the problem? As just above, certainly the order with which the observations are presented cannot have any bearing on the answer?

What assumptions are incorrect? Or are there some incorrect assumptions that have not been revealed yet?

Reversing the problem does not seem to make a difference (the moving FOR sees photons go through two slits together and result in a pattern, the stationary FOR sees photons go through single slits in sequence and sees no pattern).

 

[Dale]

They will reach at the same time, that is why there is an interference pattern, which I am not in doubt for. But, according to the quantum M interpretation, it is just a single slit experiment for the slit observer

Closing a slit doesn't instantaneously change the wave function over all space. Similarly, opening a slit doesn't instantaneously change the wave function over all space. Saying "QM" doesn't magically change the problem significantly. Doc Al's post 11 is applicable.

 

[Mentz114]

Mentz114, if both must see the same thing (pattern or no pattern), which is it, based on the presentation of the problem? As just above, certainly the order with which the observations are presented cannot have any bearing on the answer?

I don't know what the observers will see because I can't work out the arrangement of slits, screen and emitters. But all observers will see the same pattern, whether it is dots or bars.

 

[Adel Makram]

 

[Mentz114]

Only one pair of slits is necessary. Have a look at this

http://en.wikipedia.org/wiki/Double-slit_experiment

If the ground observer sees an interference pattern on his screen, then so will the train observer.

 

[Adel Makram]

Only one pair of slits is necessary. Have a look at this

http://en.wikipedia.org/wiki/Double-slit_experiment

If the ground observer sees an interference pattern on his screen, then so will the train observer.

again my question is not whether the slit-observer sees a pattern or not! but how he interprets what he sees if he consider the experiment a single-slit experiment not a double one?

 

[Mentz114]

again my question is not whether the slit-observer sees a pattern or not! but how he interprets what he sees if he consider the experiment a single-slit experiment not a double one?

I don't understand the setup. Why are there 4 slits ? How are the slits opening and closing ?

However, from the principles of relativity and simple ray-tracing, whatever is seen by one observer ( say the one at rest wrt the slits) will be seen by all.

The reason is that if a beam goes through a slit in one frame it will do so in all frames, because the coincidence in space and time of the beam and the slit is absolutely invariant. This applies to any arrangement of light paths, slits screens and whatever.

How many times do you have to be told ?

 

[Adel Makram]

you are responding to a question: will the slit-observer see a pattern or no? You are still did not get the point. sorry

 

[Adel Makram]

There is a difference between the physical phenomena and the observer interpretation. As in Einstein thought experiment. The observer in the middle of the moving train receives the light signal from the front end before the back end. This is a physical phenomena which is also seen by the ground observer. The interpretation is different, for the train observer, the event of light striking the front end happens before the back end. while for the ground observer, the mid-train observer moves toward the light from the front end faster than from the back end. that is the interpretation which causes the principle of relativity of simultaneity ,,, just try to apply the same logic in my experiment.

 

[Adel Makram]

and forget about the 2 slits near the source, let's make them just one big window :)

 

[Adel Makram]

the difference between the 2 thought experiments, is that in the Einstein`s one, the time of events in both ends of the train does not depend on the physical phenomena of receiving the light from both ends by the mid-train observer. But in y experiment, the double slit experiment tells us that unless you let the 2 slits open at the same time, you will never get a pattern. The pattern is a fixed phenomena but the opening of 2 slits at the same time is different. It is a single slit experiment for the slit-observer, I hope you get it this time

 

[Adel Makram]

https://www.physicsforums.com/attachment.php?attachmentid=42989&stc=1&d=1327254325

 

[Mentz114]

the difference between the 2 thought experiments, is that in the Einstein`s one, the time of events in both ends of the train does not depend on the physical phenomena of receiving the light from both ends by the mid-train observer. But in y experiment, the double slit experiment tells us that unless you let the 2 slits open at the same time, you will never get a pattern. The pattern is a fixed phenomena but the opening of 2 slits at the same time is different. It is a single slit experiment for the slit-observer, I hope you get it this time

The interference pattern needs only that the slits are both open when the light reaches them, not on the perception of their simultaneous opening by another observer.

Thus, the pattern will be there whether or not an observer sees the slits open at the same time.

 

[Adel Makram]

The interference pattern needs only that the slits are both open when the light reaches them, not on the perception of their simultaneous opening by another observer.

Thus, the pattern will be there whether or not an observer sees the slits open at the same time.

I guess the slit-observer will disagree with you about that statement. For him, the pattern will form only when the 2 slits open at the same time

 

[Adel Makram]

Put yourself instead of the slit-observer. You see A open and closed before B open. You will also see a pattern on an outer screen from your window. For you, the slit is an inertial FOR and the law of physics will apply there perfectly. Would you conceive the pattern is formed on the outer screen because may be some other observer sees the 2 slits open at the same time and therefore the pattern forms?

 

[Mentz114]

I guess the slit-observer will disagree with you about that statement. For him, the pattern will form only when the 2 slits open at the same time

The diagram shows a 2 slit setup. P and Q are bright spots, where the interfering beams are in phase. A and B are observers. The slits open for a small time simultaneously from A's point of view. Observer B does not see the slits open at the same time¹. Will B see the same pattern as A, or something different ?

Nothing is moving in this setup.

[1] if the slits are open for time T, then if T< (SB-S'B)/c then B will see one slit open and close before the other opens.