- #1
Saitama
- 4,243
- 93
Homework Statement
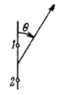
A system illustrated in the figure consists of two coherent point sources 1 and 2 located in a certain plane so that their dipole moments are oriented at right angles to that plane. The sources are separated by a distance d, the radiation wavelength is equal to ##\lambda##. Taking into account that the oscillations of source 2 lag in phase behind the oscillations of source 1 by ##\phi## (##\phi<\pi##), find the angles ##\theta## at which the radiation intensity is maximum.
Homework Equations
The Attempt at a Solution
Let the radiations from the sources ##S_1## and ##S_2## interfere at a point P. As the radiation from ##S_1## is already ahead by the given phase, I have
$$S_2P=S_1 P+d\cos\theta-\frac{\phi \lambda}{2\pi}$$
For constructive interference,
$$S_2P-S_1P=n\lambda$$
But solving the above equations doesn't give the right answer.