GatoGordo
- 1
- 0
As you can see we have 3 media here. Only focus on the glass and coating medium. Assume an incident ray comes from the air medium and is refracted inside the glass and then it is refracted again in the coating medium. The x angle is the angle inside the glass medium. In this case, if the incident ray,from the air, enters the glass it will create a refracted ray with an angle. This is the x angle. Now, let's say I want the refraction angle of the coating medium to be 90°. Why do I have to subtract 90° from the x angle to achieve this?
nglasssin(90°−x)=ncoatingsin(90°)
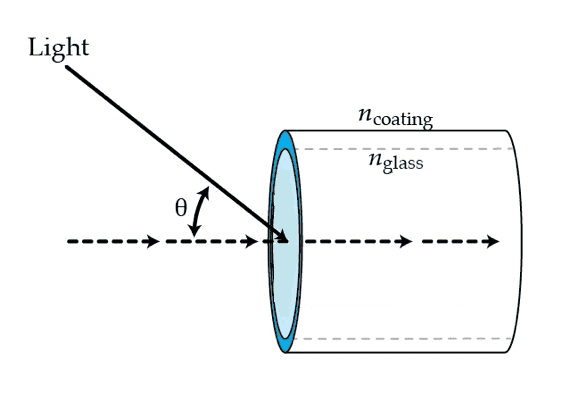
nglasssin(90°−x)=ncoatingsin(90°)
Last edited by a moderator: