- #1
ozgur(tr)
- 3
- 0
When I plot the isenthalpic curves in T-P plane, I see isenthalpic curves are not well defined in the lower temperature region in T-P plane. Inside the inversion curve Joule-Thomson coefficient is positive so gas cools and outside of the inversion curve Joule-Thomson coefficent is negative so gas warms. Also we know heat capacity at constant pressure is always positive and change of pressure is always negative. It means that change of temperature plays a role on sign of Joule-Thomson coefficient. But below the lower inversion temperature, Joule-Thomson coefficient is positive in my plot. I see other T-P planes on the internet or in the textbooks but they are well behaved in the T-P plane. Joule-Thomson coefficient is negative below the lower curve. I am not sure whether other plotts are experimental or not. Maybe I made a mistake or van der Waals EOS is not well defined for lower inversion curve or low temperature isenthalpic curve. For example, isenthalpic curves are well defined in the top of the upper inversion curves in my plot. Here I share my plot and another plot.
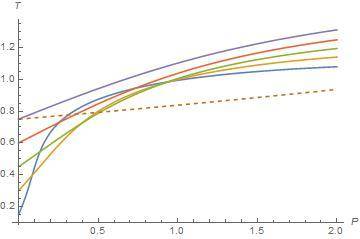

In my plot, dashed line corresponds to inversion curves and other lines correspond to isenthalpic curves. I only share a small region. Below the lower inversion curve (dashed line), slope are positive so Joule-Thomson cofficient is positive but it must negative. Is it my mistake or van der Waals EOS is not well defined in this region?
In my plot, dashed line corresponds to inversion curves and other lines correspond to isenthalpic curves. I only share a small region. Below the lower inversion curve (dashed line), slope are positive so Joule-Thomson cofficient is positive but it must negative. Is it my mistake or van der Waals EOS is not well defined in this region?