Learnphysics
- 92
- 0
Homework Statement
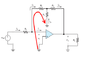
Find Vo/Vin.I understand perfectly how to do this question. It simply involves an application of ohm's law to find i1, then KVL around the first loop. KCL at the top, and KVL around the second loop. Then to solve simultaneously.
My issue however Is why the mechanics of KVL work in this case. We were taught that KVL required a closed loop, and the voltages needed to sum to zero. The diagram seems not be a closed loopIn the textbook example we say the KVL of those loops are:
Vin + i2(R2) -i3*R3 = 0.
(Vin = 0, due to a virtual short circuit)
I understand i2*R2 is the voltage drop across resistor 2. But for -i3*r3, wouldn't we also need to factor in the current i4 that's circulating around the neighboring loop? (as we'd do in mesh analysis?).
Also why are we adding the voltage of Vin when it isn't in the loop at all? It seems like we're simply adding the voltage of a certain point, as opposed to the voltage drop across a certain element.
I understand Op-amps, virtual short circuits, and such, this problem is really just focused around the circuit analysis of the feedback loop.
Thank you.
Last edited by a moderator: