Sokolov
- 14
- 1
- Homework Statement
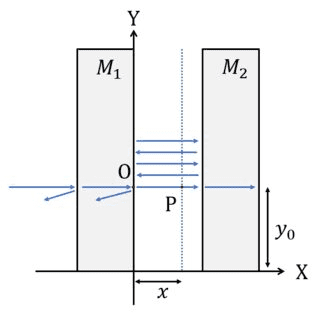
- Two flat mirrors of the same reflectance ##R## are separated from each other by a distance ##d## in the air (##n=1##). A monochromatic beam of wavelength λ, linearly polarised, falls perpendicularly on the left face of ##M_1##, entering the space between the two mirrors.
Let's suppose that the intensity when the beam crosses the right surface (point ##O##) of the first mirror is ##I_0##. Calculate the irradiance at a point ##P(x,y_0)##.
- Relevant Equations
- Fresnel's equations
The setup of the problem is shown in the image below.
I know that I must add all the contributions of each reflected ray and that its amplitude will be reduced by a factor ##r## each time it is reflected. So after the n-th reflection, its amplitude will be ##E_0r^n##, with ##E_0## the amplitude at the point ##O##and ##r## the coefficient of reflection for the amplitude. However, I'm not sure about how to introduce the phase, ##e^{i(ωt−kx+δ_0)}## for each contribution.
Could anyone give me please a hint?
I know that I must add all the contributions of each reflected ray and that its amplitude will be reduced by a factor ##r## each time it is reflected. So after the n-th reflection, its amplitude will be ##E_0r^n##, with ##E_0## the amplitude at the point ##O##and ##r## the coefficient of reflection for the amplitude. However, I'm not sure about how to introduce the phase, ##e^{i(ωt−kx+δ_0)}## for each contribution.
Could anyone give me please a hint?
Last edited: