Since
https://www.physicsforums.com/showpost.php?p=2729969&postcount=485".
As I've previously noted, it's not a "probability" being described as negative, it's possible case instance E(a,b) of a probability P(A,B|a,b). To explain the different between a "possible case instance" and a "probability", consider a coin toss. The "probability" of a heads or tails is 50% each. A "possible case instance" will be either a heads or a tails, but no "probability" is involved after the coin toss and we know which side the coin landed on. What being compared is a large group of deterministically selected case instances.
Thus saying that case instances where the coin did in fact land on tails negatively interferes with heads is true, but makes no sense in terms of "probabilities". It's a case instance, not a probability. By itself this doesn't fully describe the negative [strike]probabilities[/strike] possibilities described on the "negative probabilities" page, because there is still too many negative possibilities to account for in coin tosses.
As is well known, in the derivation of Bell's inequalties, negative possibilities
only occur in case 'instances' where detections are more likely in only one of the detectors, rather than neither or both. So far exactly as you would expect in coin tosses. To understand where the extra coin tosses c0me from we need to look at a definition.
1) Bell realism - An element of reality is defined by a predictable value of a measurement.
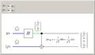
Have have 2 measuring instruments A and B, which each consist of a polarizer and a photon detector. Each measure is considered an element of reality, per Bell realism, such that a measure by each of our 2 measuring instruments constitutes 2 elements of reality. Now we are going to emit a single photon at our detectors. Only detector A has a particular polarization setting, and detector B is not another detector, but another setting we could have chosen for detector A, i.e., a counterfactual measurement.
Now, by definition we are looking for 2 elements of reality, i.e., predictable measures per Bell realism. Yet if A detects our single photon, we know B can't, and visa versa. But if counterfactually both A and B was in principle capable of separately detecting that one photon, we are allowed to presume that only sometimes did A and B both see the photon (since we can call it both ways counterfactually), and sometimes not. So if that counterfactual measure can sometimes see the same photon we are required to call that a separate element of reality per Bell Realism, even though it's the same photon. Yet that requires us to also call the times A detected the photon but B didn't 2 separate elements of reality also.
If we call it the other way, and call both measurements the same element of reality per photon, it makes sense in those case where one detector detects the photon, but not the other. But violates Bell realism in cases where both detectors were capable of detecting that same photon. The negative possibility page presumes each measurement represents it's own distinct element of reality, which makes sense in those cases where both A and B could have detected the same photon. Thus, in those cases where our single photon can't counterfactually be detected by both detectors, it appears as if reality itself has been negatively interfered with.
Objections:
But we are talking statistics of a large number of photons, not a single photon. The negative probabilities are of a large number of detections.
True, but
by academic definition, the large number of cases where derived from the special cases E(a,b) of the general probability P(A,B|a,b). It's tantamount to flipping a coin many times, taking all the cases where E(a,b)=tails, and calling that a probability because we are dealing with many cases of tails, rather than just one.
This argument is contingent upon a single assumption, that a single photon can 'sometimes' be 'counterfactually' detected by the same detector with a different polarization setting. I empirically justify this by the following empirical facts:
1) A polarizer will pass 50% of all 'randomly' polarized light.
2) A polarizer set at a 45 degree angle to a polarized beam of light will pass 50% of the light in that beam.
Now this is perfectly well described in QM and HUP, and this uncertainty is a LOCAL property of the individual photon itself. In QM, polarization is also perfectly well described as a quantum bit, where it can have values between 0 and 1. It is these partial values between 0 and 1 that allows the same photon to 'sometimes' be counterfactually detected with multiple polarizer settings. Yet this bit range is still a LOCAL property of the bit/photon.
We only have to accept the reality of HUP as a real property of the LOCAL photon polarization bit to get violations of Bell realism (a distinct issue from correlations). Yet the fact that correlations exist at all, and anti-twins (anti-correlated particles) can repeat the same response to polarizers deterministically, even with offsets in the 0/1 bits, indicates that as real as HUP is, it doesn't appear to be fundamental. So in this conception we have real LOCAL bit value ranges via HUP, legitimizing the QM coincidence predictions, with correlations that indicate HUP is valid, but not fundamental. The LOCAL validity of HUP is enough to break Bell's inequalities. While the breaking of Bell realism itself, due to LOCAL HUP, breaks the negative "possibility" proof.
The one to one correspondence between an element of reality (photon) and a detection is broken (Bell realism), when counterfactually a different detector setting can sometimes detect the same photon, and sometimes not. It does not explicitly break realism wrt the reality and locality of the photon itself. Detector and counterfactual detector is, after all, effectively in the same place.