Bernoulli's Equation is fundamentally related to the conservation of mechanical energy, particularly under specific conditions such as along a streamline, inviscid flow, steady flow, and constant density. The equation expresses energy per unit volume rather than total mechanical energy, which means it cannot be directly equated to E = constant. Instead, integrating Bernoulli's Equation over a volume along a streamline reveals that energy is conserved within that volume. For ideal fluids, the equation can be represented as ##\frac{1}{2} v^2 + w + gz = \text{const}##, where ##w## is the enthalpy per unit mass and ##u## is the internal energy per unit mass.
PREREQUISITESStudents and professionals in engineering, particularly those specializing in fluid mechanics, as well as physicists and researchers interested in the principles of energy conservation in fluid systems.
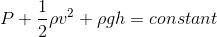
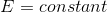is only true for a fluid with constant density ##\rho##. In general, if the fluid is ideal, we have ##\frac{1}{2} v^2+w+gz=\rm{const}.## along a streamline for a steady flow where ##w=u+p/q## is the enthalpy per unit mass and ##u## is the internal energy per unit mass. So we have a term related to the internal energy of the fluid which can still be interpreted as mechanical if you consider it as the sum of mechanical energies of the molecules, but it is not related to the macroscopic motion of the fluid.