Anna57
- 4
- 0
- TL;DR
- A question regarding the validity of the relationship $$dQ=TdS$$ for all quasi-static processes. Based on Callen's Thermodynamics.
Hello!
I am currently reading the second edition of Callen's Thermodynamics and an Introduction to Thermostatistics, and I have a question regarding Callen's definition of quasi-static. On page 96, Callen says:
I am currently reading the second edition of Callen's Thermodynamics and an Introduction to Thermostatistics, and I have a question regarding Callen's definition of quasi-static. On page 96, Callen says:
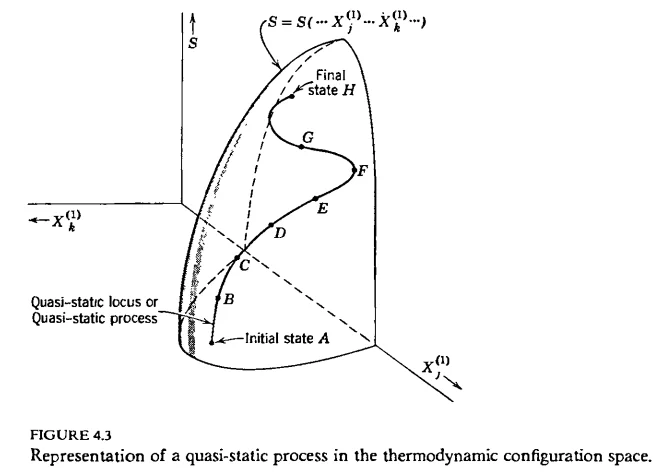
Another way of characterizing Callen's definition is that a process is quasi-static if it traces out a continuous curve in the system's configuration space. So far it's all well and good. A little later, Callen claims that the identification of $$TdS$$ as the heat transfer is only valid for a quasi-static process. In seemingly the rest of the book, he takes this to be a necessary criterion for quasi-staticity. A process which does not obey $$dQ=TdS$$, no matter how well it seems to fit the original definition in terms of equilibrium states, is apparently not quasi-static. I am having a lot of trouble understanding how Callen draws this conclusion as it is not motivated and other motivations later on are predicated on this being true. Is it possible to prove, based on the definition of quasi-staticity given above, that it necessarily follows that $$dQ=TdS$$ for any, arbitrary quasi-static process? I have searched far and wide but cannot find any general proof. I am having trouble believing it is even true, and sources online even seem to disagree.Consider an arbitrary curve drawn on the hypersurface of Fig. 4.3*, from an inital state to a terminal state. Such a curve is known as a quasi-static process. A quasi-static process is thus defined in terms of a dense succession of equilibrium states.
*Fig. 4.3, the hypersurface defined by the entropy function graphed in its configuration space