Is Concatenating Matrices Possible for Different Mesh Sizes?

[qwuasi]

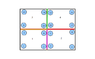
I have a mesh (2-by-2) which is numbered 1:16.

[URL]http://www.flickr.com/photos/moorekwesi/5454749337[/URL]

A = [1 2 5 6; 3 4 7 8;9 10 13 14;11 12 15 16] ;

i want to create a matrix of the nodes from the element and it's neighbouring nodes.
This is for a 2-by-2 and hope to implement it also for say 15-by-15.
>>
The 2-by-2 results
I2 = [A(1,:) A(2,1) A(2,3) A(3,1) A(3,2) ;
A(2,:) A(1,2) A(1,4) A(4,1) A(4,2) ;
A(3,:) A(4,1) A(4,3) A(1,3) A(1,4) ;
A(4,:) A(3,2) A(3,4) A(2,3) A(2,4)]

 

[tedbradly]

Is this matlab? Also, all the jargon you're using makes what you want unclear to me. What do you consider a node and what do you consider a neighboring node? Is A your "2 by 2 mesh," whatever that is?

 

[qwuasi]

Homework Statement

Given a square grid ( n-by-n) with numbering 1:4n² from the figure attached
(eg. n=2), the matrix: A = [1 2 5 6; 3 4 7 8;9 10 13 14;11 12 15 16] which corresponds
to the elements,ie row 1 corresponds to element 1,etc. is generated.i
want to create a new matrix such that for every element,i'll have the nodes
of the element and nodes from other elements which share a common edge.
This is the final result in this case is:
I2 = [A(1,:) A(2,1) A(2,3) A(3,1) A(3,2) ; A(2,:) A(1,2) A(1,4) A(4,1) A(4,2) ;
A(3,:) A(4,1) A(4,3) A(1,3) A(1,4) ; A(4,:) A(3,2) A(3,4) A(2,3) A(2,4)];

The Attempt at a Solution

I created matrix B (all the edges of A) and C (to get a column representation
of the edges).
B=[A(:,[1 3]) ; A(:,[2 4]) ; A(:,[1 2]) ; A(:,[3 4]) ] ' ;
C = reshape(B , 8 , [ ] ) ' ;

 

[qwuasi]

The nodes are colored BLUE and edges red,green,...Each element consist of the four nodes in that box. eg A(1) = {1 2 5 6},A(2) = {3 4 7 8}.The final solution is made of nodes in an element and and nodes (usually 2nodes) from neighbouring elements which share a common edge(straight line) eg for element 1: E(1) = {1 2 5 6 3 7 9 10}.
E(2) = {3 4 7 8 2 6 11 12}...likewise for E(3) and E(4).

I hope this helps.

Thank You

 

[tedbradly]

I just finished the algorithm. It can handle N = 15 instantly, and I verified it works correctly with N = 2. However, I'm not sure if it actually gets the right answers for anything beyond N = 2. Have fun.

N = 15;
for meshR = 1:N
    for meshC = 1:N
        r = (1:2)+(meshR-1)*2;
        c = (1:2)+(meshC-1)*2;
        ans1 = r + (c(1)-1)*N*2;
        ans2 = horzcat(ans1, ans1+N*2);
        if meshR < N %add contact to right
            ans1 = r(2) + 1 + (c(1)-1)*N*2;
            ans2 = horzcat(horzcat(ans2, ans1),ans1+N*2);
        end
        if meshR > 1 %add contact to left
            ans1 = r(1) - 1 + (c(1)-1)*N*2;
            ans2 = horzcat(horzcat(ans2, ans1),ans1+N*2);
        end
        if meshC < N %add contact above
            ans1 = r + c(2)*N*2;
            ans2 = horzcat(ans2, ans1);
        end
        if meshC > 1 %add contact below
            ans1 = r + (c(1)-2)*N*2;
            ans2 = horzcat(ans2, ans1);
        end
        I2{N*(meshC-1)+meshR} = ans2;
    end
end
%for k = 1:N^2
%   I2{k}
%end

 

[qwuasi]

Dear Sir,
Thank you so much for your assistance.For two months,i've struggled with this.It forms 20% of my thesis work.Seeing the results has given me good health.

Thank You.

 

[tedbradly]

Dear Sir,
Thank you so much for your assistance.For two months,i've struggled with this.It forms 20% of my thesis work.Seeing the results has given me good health.

Thank You.

No problem. If you want to cite me, pm me and I'll give you my real name. But I don't care if you use my algorithm without citation.