chagular
- 5
- 0
For a real gas (non-ideal gas) in a reversible process, the way to calculate \Delta{S} should also be independent to path simply because entropy is a state function.
However, I got strange solution while taking different path.
Here is the condition:
1. Equation of state (EOS) for the real gas could be arbitrary (but actually not ideal)
2. The constant volume heat capacity is only the function of temperature or a constant, i.e., C_V=f(T) only.
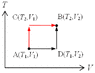
3. State changes from A(T_1,V_1) to B(T_2,V_2).
As illustrated (attached figure). Basically, there're two simple paths for calculation.
(1) The black route: A-D-B
(2) The red route: A-C-B
The total differential of entropy as function of T and V is:
dS=\frac{C_V}{T}dT+\left(\frac{\partial P}{\partial T}\right)_VdV.
Both entropy change in constant-V process A-C and D-B are identical:
\Delta{S}=\int^{T_2}_{T_1}\frac{C_V}{T}\,dT.
But I can't prove that the rest two constant T process paths have same contribution as encountering a real gas:
(1) for A-D (in black route)
\Delta{S_{AD}}=\int^{V_2}_{V_1} \left.\left(\frac{\partial P}{\partial T}\right)_V\right|_{T_1}\,dV
(2) for C-B (in red route)
\Delta{S_{CB}}=\int^{V_2}_{V_1} \left.\left(\frac{\partial P}{\partial T}\right)_V\right|_{T_2}\,dV
It's obvious that \Delta{S_{AD}} is not identical to \Delta{S_{CB}} if \left(\frac{\partial P}{\partial T}\right)_V is function of both V and T. Such a situation could happen for almost all real gas.
The result obtained above is opposed to the fundamental knowledge: entropy is a state function. Regardless of the integration difficulty that might encounter as we could always use numerical integration especially when analytical EOS is available. What is wrong with my derivation?
However, I got strange solution while taking different path.
Here is the condition:
1. Equation of state (EOS) for the real gas could be arbitrary (but actually not ideal)
2. The constant volume heat capacity is only the function of temperature or a constant, i.e., C_V=f(T) only.
3. State changes from A(T_1,V_1) to B(T_2,V_2).
As illustrated (attached figure). Basically, there're two simple paths for calculation.
(1) The black route: A-D-B
(2) The red route: A-C-B
The total differential of entropy as function of T and V is:
dS=\frac{C_V}{T}dT+\left(\frac{\partial P}{\partial T}\right)_VdV.
Both entropy change in constant-V process A-C and D-B are identical:
\Delta{S}=\int^{T_2}_{T_1}\frac{C_V}{T}\,dT.
But I can't prove that the rest two constant T process paths have same contribution as encountering a real gas:
(1) for A-D (in black route)
\Delta{S_{AD}}=\int^{V_2}_{V_1} \left.\left(\frac{\partial P}{\partial T}\right)_V\right|_{T_1}\,dV
(2) for C-B (in red route)
\Delta{S_{CB}}=\int^{V_2}_{V_1} \left.\left(\frac{\partial P}{\partial T}\right)_V\right|_{T_2}\,dV
It's obvious that \Delta{S_{AD}} is not identical to \Delta{S_{CB}} if \left(\frac{\partial P}{\partial T}\right)_V is function of both V and T. Such a situation could happen for almost all real gas.
The result obtained above is opposed to the fundamental knowledge: entropy is a state function. Regardless of the integration difficulty that might encounter as we could always use numerical integration especially when analytical EOS is available. What is wrong with my derivation?