Is it necessary to calculate acceleration for this problem?

[Benjamin_harsh]

Homework Statement

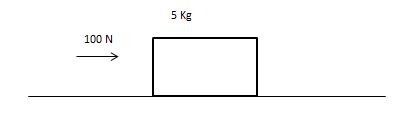
A force of 100N applied to a body which has 5kg mass. Coefficient of static friction($μ_{s}$) is 0.60 and Coefficient of kinetic friction($μ_{k}$) is 0.55.

Relevant Equations

Acceleration from Net force, $a = \large \frac{70.6}{5}$ = $14.1 \;m/sec^{2}$ to the right.

Acceleration from Net force, $a = \large \frac{73.06}{5}$ = $14.61 \;m/sec^{2}$ to the right.

A force of 100N applied to a body which has 5kg mass. Coefficient of static friction(μs) is 0.60 and Coefficient of kinetic friction(μk) is 0.55.

A) $μ_{s} = 0.60$; $μ_{k} = 0.55$
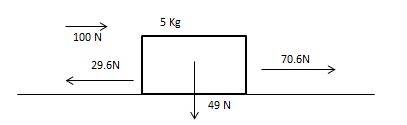
$F_{s}^{max} = F_{n}*μ_{s}$
$F_{s}^{max} = 49*0.60 (F_{n} = 9.8 \;m/sec^{2} *(5kg) = 49N)$
$F_{s}^{max} = 29.4 N$
Net force, $F_{net} = 100 – 29.4N = 70.6N$
Acceleration from Net force, $a = \large \frac{70.6}{5}$ = $14.1 \; m/sec^{2}$ to the right.

Frictional force = $F_{n}*μ_{k}$
Frictional force = $49*(0.55) = 26.95N$
Net Force, $F_{net} = 100 – 26.95 = 73.05N$

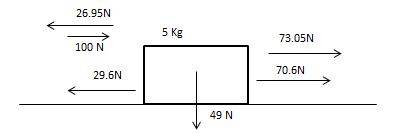
Acceleration from Net force, $a = \large \frac{73.06}{5}$ = $14.61 \; m/sec^{2}$ to the right.

 

[FactChecker]

First, calculate if the force is great enough to overcome the static friction. If not, it will not move. If it is great enough, use the kinetic friction to calculate whatever the problem asks you to calculate. Your statement of the problem is not complete. You do not say what it asks you to calculate.