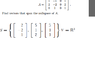pyroknife
- 611
- 4
I attached 2 problems.
For problem #1. I want to make sure I'm on the right track, to find the span of Null(A), i need to put matrix A in RREF form. By doing so I get
x1=-2t
x2=-t
x3=s
x4=u (using u because I'm using t to denote transpose)
where x1 to x4 is for each respective column. x3 and x4 turns out to be the free variables (columns 3 and 4).
This gives the vectors s[0 0 1 0]^t and u[-2 -1 0 1]^t
Thus the vectors that span Null(A) = [0 0 1 0]^t and [-2 -1 0 1]^t
The second problem is for the 2nd matrix S in the attached file. The question asks, determine whether S is a basis for the vector space V.
To do this, I think I need to take the determinant of the 3 vectors in S. This gives a determinant of "-2." This implies that the vectors are linearly indepdent and thus they form a basis for V=R^3.
Did i do these 2 problems correctly?
For problem #1. I want to make sure I'm on the right track, to find the span of Null(A), i need to put matrix A in RREF form. By doing so I get
x1=-2t
x2=-t
x3=s
x4=u (using u because I'm using t to denote transpose)
where x1 to x4 is for each respective column. x3 and x4 turns out to be the free variables (columns 3 and 4).
This gives the vectors s[0 0 1 0]^t and u[-2 -1 0 1]^t
Thus the vectors that span Null(A) = [0 0 1 0]^t and [-2 -1 0 1]^t
The second problem is for the 2nd matrix S in the attached file. The question asks, determine whether S is a basis for the vector space V.
To do this, I think I need to take the determinant of the 3 vectors in S. This gives a determinant of "-2." This implies that the vectors are linearly indepdent and thus they form a basis for V=R^3.
Did i do these 2 problems correctly?