Is the Acceleration of the Universe Expansion accelerating?

[Swimmingly!]

I watched an interview with Edward Witten some time ago and something he said surprised me.
(http://www.youtube.com/watch?v=eEutI_JKr7A) 3:25
"Which in GR causes the acceleration of the universe to accelerate."
Did he literally meant this?
I'm not sure how accurately you can talk about the volume of the universe, but am I interpreting what he said right?
Is

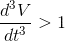true?
I'm aware it is true for the second derivative but for the third too?

V=Volume

I hope this is in the right section. Thanks.

 

[phyzguy]

If the Lambda-CDM model is correct, the universe will become more and more dominated by the cosmological constant as it expands. When it is lambda-dominated, it expands exponentially, so the scale factor goes like a~exp(K t). Since the volume V ~ a^3, the volume is also expanding exponentially. For an exponential function, all derivatives are increasing exponentially. So the answer to your question is yes, the third derivatives and all higher derivatives are increasing as well. See:

http://en.wikipedia.org/wiki/Friedmann_equations

 

[Swimmingly!]

If the Lambda-CDM model is correct, the universe will become more and more dominated by the cosmological constant as it expands. When it is lambda-dominated, it expands exponentially, so the scale factor goes like a~exp(K t). Since the volume V ~ a^3, the volume is also expanding exponentially. For an exponential function, all derivatives are increasing exponentially. So the answer to your question is yes, the third derivatives and all higher derivatives are increasing as well. See:

http://en.wikipedia.org/wiki/Friedmann_equations

That answers it. Thank you.