Tekneek
- 70
- 0
Why is the limit not just infinity?
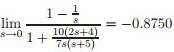
wouldn't it be (1-infinity)/(1+infinity)?
wouldn't it be (1-infinity)/(1+infinity)?
mfb said:Why should "-infinity/infinity" be infinity?
What is the limit of
$$\lim_{s \to 0} \frac{\frac{-1}{2}}{\frac{2}{s}}$$?
mfb said:Sorry typo, this is the formula I meant:
$$\lim_{s \to 0} \frac{\frac{-1}{s}}{\frac{2}{s}}$$
But the more important part was the first question.
That is not the point. It follows the "-infinity/infinity" type. It is easy to simplify it here to see the limit is not infinity, so your original idea cannot work - that was the purpose of the example.Tekneek said:For that formula it would be -1/2.
I don't understand that question.I was thinking it would be infinity because you really can't put down a number with it unless maybe it is 1?
Okay.EDIT: Nvm go it. It ends up being -35/40. Thnx
Tekneek said:Why is the limit not just infinity?
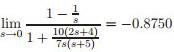
wouldn't it be (1-infinity)/(1+infinity)?
No, check your algebra. The answer in post #1 (-7/8) is correct.Garrulo said:The limit is of (s-1)/(s+(10*(2s+4)/7(s+5) that doing s=0 result in -7/15