Is the Solution for Finding Hall Voltage Correct?

[PhysicsTest]

Homework Statement

a. Find the magnitude of the Hall voltage VH in an n-type germanium bar used in fig, having majority-carrier concentration ND = 10^17 /cm^3. Assume Bz=0.1 Wb/m^2, d=3 mm, Ex=5V/cm.
b. What happens to VH if an identical p-type germanium bar having NA=10^17/cm^3 is used in part a?

Relevant Equations

$V_H = Ed=Bvd = \frac{BJd} {\rho w}$

The question is to find the Hall voltage

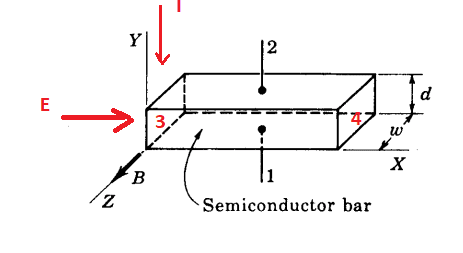
The magnetic field is in the +ve Z-direction, the electric field is in the +ve X-direction, the current will be in -ve Y direction.
There are many equations to find the hall voltages $V_H = Ed=Bvd = \frac{BJd} {\rho w}$. But i find the equation $V_H = Ed$ to solve and other parameters are not much of use.
a. n-type 4 will be more negative than 3 and $V_H = 5*0.3V = 1.5V$
b. p-type 4 will be more positive than 3 and $V_H = 5*0.3V = 1.5V$
Is the solution correct, or missing something?

 

[Delta2]

No I don't think it is correct. The E-field in the x direction $E_x=5V/cm$ is responsible for creating the current density $J=\sigma E_x$ according to Ohm's law.
It is the E-field in the y-direction $E_y=Bv$ that creates the hall voltage.

 

[Tom.G]

No I don't think it is correct. The E-field in the x direction $E_x=5V/cm$ is responsible for creating the current density $J=\sigma E_x$ according to Ohm's law.
It is the E-field in the y-direction $E_y=Bv$ that creates the hall voltage.

I disagree with the disagreement.

The interaction of the current flow and B field creates a Hall voltage that is perpendicular to both, think Lorentz force. The problem statement specifies the direction of both current direction, X-axis, and B-field direction, Z axis. This leave only the Y axis for the Hall voltage. Note that the Terminals "1" and "2" (sense terminals) are in the Y dimension. (But that graph sure shows an unusual axes orientation.)

As for the numerical solution, I have no idea! That must be left to those that have studied this in more detail.

 

[Delta2]

I disagree with the disagreement.

The interaction of the current flow and B field creates a Hall voltage that is perpendicular to both, think Lorentz force. The problem statement specifies the direction of both current direction, X-axis, and B-field direction, Z axis. This leave only the Y axis for the Hall voltage. Note that the Terminals "1" and "2" (sense terminals) are in the Y dimension. (But that graph sure shows an unusual axes orientation.)

As for the numerical solution, I have no idea! That must be left to those that have studied this in more detail.

I don't understand where you disagree with me. We both say that the current is in the x-axis and that the hall voltage is in the y-axis. The way the OP did the calculation implies that the hall voltage is along the x-axis.

 

[Tom.G]

Perhaps it is a nomenclature difference.

Re-reading your two posts I see that we agree on the orientation of the Hall voltage.

I was thrown off by the use of 'E-field' being the cause of the Hall voltage. I was thinking of 'fields' being externally applied things, rather than being electron paths.

Sorry for any unnecessary confusion.

Tom

 

[Delta2]

I was thrown off by the use of 'E-field' being the cause of the Hall voltage

I said that this E-field is in the y-direction. Of course the mechanism of hall voltage is known to me, it is not the electric field the real cause. It is the Lorentz force $(\mathbf{v}\times\mathbf{B})q$ that creates charge separation and a coulomb electric field $\mathbf{E_H}$ such that $$\mathbf{E_H}q=(\mathbf{v}\times\mathbf{B})q$$ and the hall voltage is of course $$V_H=E_Hd$$

 

[PhysicsTest]

Still not able to solve, not sure if some of the data is missing or to assume something. I understood the above discussion
$V_H = \frac{BJd} {\rho w}$ ->eq1
$J = \sigma E_x$ ->eq2
substitute eq2 in eq1
$V_H = \frac{B\sigma E_x} {\rho w}$ ->eq3
If conduction primarily due to charges of one sign, the conductivity $\sigma$ is related to mobility $\mu$ by
$\sigma = \mu \rho$ -> eq4
substitute in eq3 to give
$V_H = \frac{B\mu E_x} {w}$ -> eq5
Now i do not know the value of $\mu$. Is the above derivation correct? Can i assume its value at 300K which is a standard value i assume.

 

[Delta2]

Still not able to solve, not sure if some of the data is missing or to assume something. I understood the above discussion
$V_H = \frac{BJd} {\rho w}$ ->eq1
$J = \sigma E_x$ ->eq2
substitute eq2 in eq1
$V_H = \frac{B\sigma E_x} {\rho w}$ ->eq3
If conduction primarily due to charges of one sign, the conductivity $\sigma$ is related to mobility $\mu$ by
$\sigma = \mu \rho$ -> eq4
substitute in eq3 to give
$V_H = \frac{B\mu E_x} {w}$ -> eq5
Now i do not know the value of $\mu$. Is the above derivation correct? Can i assume its value at 300K which is a standard value i assume.

In going from Eq1 to Eq3 (using Eq2) you have forgotten $d$.
What is $\rho$? The density of charge carriers?

 

[PhysicsTest]

In going from Eq1 to Eq3 (using Eq2) you have forgotten $d$.

Sorry my mistake the eq(3) is
$V_H = \frac{B\sigma E_xd} { \rho w}$ ->eq(3)

What is $\rho$? The density of charge carriers?

Yes $\rho$ is the density of charge carriers

 

[Delta2]

I feel there is something wrong regarding the $w$ in eq(3). As far as I know $$V_H=Bvd, J=\rho v\Rightarrow V_H=\frac{BJd}{\rho}$$ so I really don't see how you get that $w$ there. Is this equation $$V_H=\frac{BJd}{\rho w}$$ taken straight from the book?

 

[PhysicsTest]

I am really confused with all these equations

Yes it is the current I not the J the current density.

 

[Delta2]

I am really confused with all these equations
View attachment 276051
Yes it is the current I not the J the current density.

Ah this settles it, yes the book is right (and I was right too in post #10). It is $$I=JS=Jdw$$ that's how the last equality is explained. ($S$ is the cross section of the semiconductor $S=dw$ according to the figure provided).
So to sum it up:
The correct (eq3) is $$V_H=\frac{B\sigma E_xd}{\rho}$$ and IF $$\sigma=\mu\rho$$ is correct then (eq3) leads to $$V_H=B\mu E_xd$$. I suppose from this last equation you can find the hall voltage, if you know $\mu$ as everything else is given.

Something else is the density of the charge carriers $N_D$ (or $N_A$) given in $cm^{-3}$ or $Cb\cdot cm^{-3}$ because the $\rho$ appearing in the above equations has units of the latter case ($Cb\cdot cm^{-3}$).

 

[PhysicsTest]

I suppose from this last equation you can find the hall voltage, if you know $\mu$ as everything else is given

But that is not given, can i assume a value?

Something else is the density of the charge carriers $N_D$ (or $N_A$) given in $cm^{-3}$ or $Cb\cdot cm^{-3}$ because the $\rho$ appearing in the above equations has units of the latter case ($Cb\cdot cm^{-3}$).

I really did not understand this.

 

[Delta2]

But that is not given, can i assume a value?

Not sure, what is given is $N_D$ or $N_A$. I think we must use those somehow (but in the correct units, see below). Look in book for table with the $\sigma$ of germanium at various temperatures. I am very unsure about the equation $\sigma=\mu\rho$.

I really did not understand this.

I am asking in what units are the $N_D$ or $N_A$ given. In the OP it seems that the units are $\frac{1}{cm^3}$ or simply $cm^{-3}$.

 

[PhysicsTest]

i am not sure if the original question is wrong, i have taken from the book as it is

This is how i derived the equations. Generally in some of the previous questions i used to see $N_D$ units as $atoms/cm^3$

 

[Delta2]

Ok i see. The only problem i see is whether the $\rho$ in this equation $\sigma=\rho\mu$ is the same quantity as the $\rho$ in this equation $V_H=\frac{B\sigma E_xd}{\rho}$
Also what is q that appears in the equation for $\sigma$ in the image above. Is it the charge of the electron?

It seems that we need $\mu$ to calculate the hall voltage...

 

[PhysicsTest]

Yes charge of the electron is "q" in the equation.

 

[Delta2]

It seems to me that $\rho=N_Dq$ or $\rho=-N_Aq$ where q the charge of electron

 

[PhysicsTest]

One question i wanted to ask is that an external voltage (electric field $E_e$) is used to drive the current I. Because of magnetic field a force is applied on the charged electrons and holes and hence the Hall voltage (Hall electric field $E_H$) is set up. Will there be a net electric field of $E_e \text{ and } E_H$ ?

 

[Delta2]

Yes there will be a net electric field from those two E-fields, but the effect of the field $E_H$ on the charge carriers is "neutralized" by the force $(\mathbf{v}\times \mathbf{B})q$ which is equal and opposite of the force $E_Hq$. So $E_H$ is like it doesn't exist for the charge carriers, it doesn't affect their motion, it doesn't make a new current if that's what you were thinking of.