Eitan Levy
- 259
- 11
Homework Statement
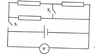
This circuit is given:[/B]
Each resistor has a resistance of 30Ω, and the electrive force is 28V.
Now we shut S1, and the voltmeter displays a value lower by 10% from the previous one.
What is the internal resistance of the voltage source?
What is the voltage between the parts of S2?
Now we shut S2 (S1 stays shut), will the voltage displayed be higher of lower than the voltage displayed when only S1 closed?
Homework Equations
V=IR
The Attempt at a Solution
My answers are:
r=(20/9)Ω (Textbook says 2Ω)
V=12.6V (Again, a different answer according).
The voltage will be lower (Textbook says higher)
The book is brand new so it has some mistakes, that's why I am asking.
Thanks in advance!
*How I reached those values:
When both switches are open no current is flowing. V=28V.
When we shut S1 the new voltage become 25.2V, that means that 25.2=28-Ir (r for internal resistance).
Now the total resistance would be (60*30)/(60+30)+r=20+r. From here we can see: I=28/(20+r)
Two equations with two parameters.
I=1.26A, r=(20/9)Ω
The current on the top branch would be I/3=0.42A
The current on the branch below would be 2I/3=0.84A
The voltage: -0.42*30+0.84*30=12.6V.
Now, when we shut both switches no current would flow through the resistor right to S2.
The combined resistance becomes (30*30)/(30+30)+r, this gives a number smaller than the combined resistance before. That means the I will be higher this time, and because V=ε-Ir, V will be smaller.
Attachments
Last edited by a moderator: