Juggernaut
- 4
- 0
Homework Statement
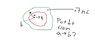
Assume we have cavity in conductor. In the cavity we have +3q charge and conductor charge is distributed uniformly and is +7q.
With Gaus law we now that E=0 inside the conductor becaus Q enclosed is 0. But I have been wondering is there potential difference from inner wall to outer wall of conductor?
There is -3q in the inner wall and +4 outer wall and inside conductor E=0 so V= constant but is there potential leap between inner and outer wall?