Is there an alternative method to solve this problem

[Casio1]

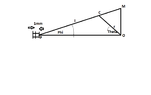
With reference to the Force Diagram, which represents a single piston cylinder rotating and producing 26NM of torque.

The technical data given is;

I = 70mm
r = 18mm
T = 26Nm
Theta = 17.13 degress
Phi = 4.34 degress

Using the diagram calculate the force on the piston Fp at 1mm before TDC.

Interestingly I can't solve this using the above data, but using trig in conjunction with the above I calculated the following angles;

Triangle OMC

M = 85.66 degress
O = 72.87 degrees
C = 21.47 degress

I worked it out like this;

PC = 18(sin 17.13) / (sin 4.34) = PM = I = 70.06 mm

The length (I) has now been proven.

Using the sine rule;

OM = 18(sin 21.47) / (sin 85.66) = 6.61

Force on piston Fp = 26 / 6.61 x 1000 = 3933 N

Once you follow it through you will see that I have not used much of the original data to solve the problem, but I am thinking there is an alternative method because I am to believe that the actual solution is

Fp = 3935 N

Although it is only two Newtons difference I could be using the wrong techniques?

 

[Sudharaka]

Hi Casio, :)

PC = 18(sin 17.13) / (sin 4.34) = PM = I = 70.06 mm

How did you equate PC and PM?

Kind Regards,
Sudharaka.

 

[Ackbach]

Hi Casio, :)
How did you equate PC and PM?

Kind Regards,
Sudharaka.

Building on that, did you have your calculator set to use degrees and not radians?

 

[Casio1]

Hi Casio, :)
How did you equate PC and PM?

Kind Regards,
Sudharaka.

Hi Sudharaka:)

Thanks for replying to the thread, I have worked out a full solution now to the problem, so will post it soon.

Kind regards

Casio

 

[Casio1]

Building on that, did you have your calculator set to use degrees and not radians?

Hi Ackbach,

I didn't adjust the calculator to radians as the unit measurements were given in degress, but I have solved it and will post full solution soon.

Kind regards

Casio

 

[Casio1]

Sorry for not replying earlier:D

I have worked on the problem and this is what I have now calculated.

With reference to the force diagram, which should be drawn as a rectangle to find the angles required.

The length of OM is;

OM = r 18(sin21.47) / (sin 85.66) = 6.6072mm

The length of "I" is calculated as;

I = PC = 18(sin 17.13) / (sin 4.34) = 70.0594 mm

The length OP is calculated as;

OP = Sqrt PC^2 - OM^2 = 70.0594^2 - 6.6072^2 = Sqrt 4856 = 69.69mm

Length of OP = OC + OP = 18 + 69.69 = 87.69mm

Force Fp = (r x F x sin(158.53))

Fp = T / r (sin 158.53) = 26 / 6.5883 = 26K / 6.5883 = 3946.4N

The compoent force acting on the piston is calculated from;

Fc = cos 4.34 = (3946.4 x cos (4.34)) = 3935.1N

I have moved on from this now and also calculated other areas like;

Diameter of the cylinder, area of the cylinder, swept volume of the cylinder, clearance colume of the cylinder, compression ratio of the cylinder, and the compression pressure:)

Casio