Is this a compound angle? What's the geometric meaning?

[xXNightEagleXx]

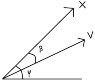
β is vehicle sideslip (angle between velocity and vehicle forward vector) ψ the angle between the trajectory tangent and vehicle forward vector. I have this equation that says

Vx * k * (cos ψ - tan β * sin ψ)

where k is trajectory curvature (1 / r) at point p.

Now i must say that I'm not proficient with compound angles at all, so I'm struggling to understand if everything inside the parenthesis is basically a compound angle. Moreover I'm struggling to visualize its geometric meaning.

Can anyone try to help me out with this one?

(I believe that k just acts as a multiplier according to the curvature so it's not the problem itself)

Thanks in advance

 

[kuruman]

I have this equation that says
Vx * k * (cos ψ - tan β * sin ψ)

That's not an equation that says anything because there are no two sides with an "equals" sign between them. Setting that aside, you can rewrite the expression as
$$V_xk\frac{\cos (\psi+\beta)}{\cos \beta}$$
Does this answer your question?