0x95
- 4
- 0
Hello,
1. Homework Statement
1) Let f(x) continuous for all x and (f(x)2)=1 for all x. Prove that f(x)=1 for all x or f(x)=-1 for all x.
2) Give an example of a function f(x) s.t. (f(x)2)=1 for all x and it has both positive and negative values. Does it contradict (1) ?
2. The attempt at a solution
1) f(x)2 = 1 → f(x)=±1 → f(x) = 1 ∨ f(x) = -1 (since f(x) can't be both)
2) There's no such function.
A step function s.t.
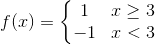
I consider incorrect since in this case f(x) =1 or f(x)=-1 not for all x but f(x)=1 for some domain and f(x)=-1 for another domain.
Is this a correct solution ?
Thank you
1. Homework Statement
1) Let f(x) continuous for all x and (f(x)2)=1 for all x. Prove that f(x)=1 for all x or f(x)=-1 for all x.
2) Give an example of a function f(x) s.t. (f(x)2)=1 for all x and it has both positive and negative values. Does it contradict (1) ?
2. The attempt at a solution
1) f(x)2 = 1 → f(x)=±1 → f(x) = 1 ∨ f(x) = -1 (since f(x) can't be both)
2) There's no such function.
A step function s.t.
I consider incorrect since in this case f(x) =1 or f(x)=-1 not for all x but f(x)=1 for some domain and f(x)=-1 for another domain.
Is this a correct solution ?
Thank you