Is this the Wavelength? (Diffraction)

[Modrisco]

I've asked this question about 4 times on yahoo but no one seems to have the brains to answer it!

Looking at the diagram:

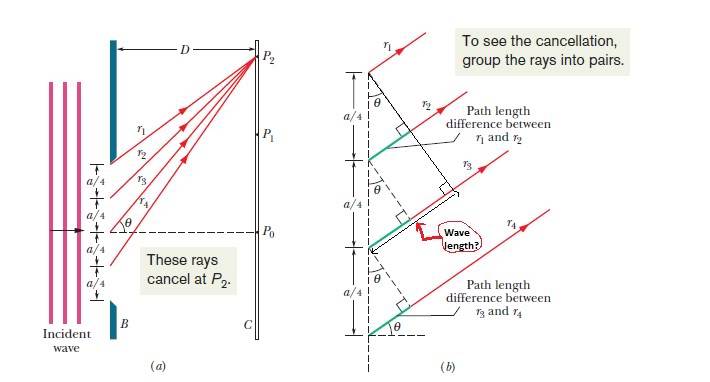
Just trying to get a better understand of "λ = asin Ѳ"

I've marked what I think is the wavelength...can someone please advise? as I'm trying to get a report done and I don't want to say the wrong thing!

If that's not the wavelength..is it the green line?

Thank you!

 

[Emilyjoint]

If pairs are cancelling out then the path difference is 1/2 wavelength.
I think the green lines are 1/2wavelength so the red+green is 1wavelength