Nope, Ich. I can’t do it. You said, a little dismissively, ‘you have all the formulae you need’. And I suppose that I do. But then I had all the formulae I needed all along, all of these formulae are in the public domain. I suppose it’s not the formulae that I am missing. I can see that a question might legitimately be raised as to exactly why I am making this post. To answer that question I might risk accusations of arrogance and claim that, on a thread that has experienced a bit of misunderstanding and some misalignment between questions asked and answers supplied, I am going to attempt to bring a little clarity; clarity of statement of the problem at least, because I can’t provide any kind of statement about the solution. The follow up question that I might then be asked is ‘clarity for whom exactly?’ And the truthful answer to that may well be ‘for no-one but myself’.
A clear statement of those formulae does add something to the clarification of the argument, so let’s just quickly state them. I have taken on board your assertion that setting c = 1 and thus stating all other velocities as a proportion of c, together with judicious use of the Lorentz factor, does have a tendency to simplify the formulae. So, in that vein:
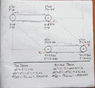
Lorentz Factor:
\gamma=\frac{1}{\sqrt{1-v^2}}
Velocity Addition:
s=\frac{v+u}{1+vu }
Length Contraction:
x’=\frac{x}{\gamma}
Time Dilation:
t’=\gamma t
In the velocity addition formula,
v is the velocity of the first body relative to the stationary frame,
u is the velocity of the second body relative to the first and
s is the velocity of the second body relative to the stationary frame.
The reason that stating these formulae provides clarity to the argument is that it enables us to classify exactly what the argument is. The derivations of these formulae are also openly available. The question of their accuracy is nothing specific to the tank track problem, and to question them is actually to question relativity theory, which in point of fact is actually against forum rules. Not that I am trying to hide behind that fact, but it is clear that a questioning of these formulae is an argument of a completely different nature. If the basic formulae are accepted, then all we are trying to achieve is an understanding of how they help to resolve the tank track problem.
My first attempt to resolve it by making use of these formulae – in post #27 – crashed in a snotty heap because of whatever it is that I am missing. Clearly, I am still missing something, but I have made some progress since then.
1. The different length contractions
I was focused on the difference in length contraction between the bottom track and the top track. There is actually a third length contraction involved, that between the front and rear wheels. I know others are going to say we already said that, but it didn’t penetrate at the time and now that I get it, I see a value in the clear statement of the length contraction differences:
If we state clearly that:
l = the uncontracted length under discussion
l_w = the wheel base, the distance from the centreline of the rear wheel to the centreline of the front wheel
l_t = the length of the top track – the length of linear forward travel
l_b = the length of the bottom track – the length of linear rearward travel
then, when the tank is stationary in front of us in the ground frame, clearly
l = l_w = l_t = l_b.
But when the tank is traveling at speed
l_w = \frac{l}{\gamma}
l_t = l {\times} \sqrt {1-s^2} and
l_b = l
To put some values on it in our example of v = 0.45c,
l_w = 0.893l
l_t = 0.663l and
l_b = l
Now it can be seen that apparently, the top track is hopelessly stretched over the wheel base and the bottom track is hopelessly loose. You explained this by taking advantage of the fact that tank tracks are usually segmented and stated that the segments, themselves length contracted, are more densely packed at the top, and uncontracted, are spaced further apart at the bottom. But the segmentation is a convenience and not really an explanation of the point. Perhaps this is not a tank track at all. Perhaps this is a continuous fabric conveyor belt stretched over two wheels, attached to the side of a body that has gained its velocity by some other means. The problem is the same. But my contention is that the conveyor belt is not really stretched at the top and hanging loose at the bottom. All we are really talking about is differences of deflection in spacetime between the conveyor top, the wheel base and the conveyor bottom relative to the ground frame.
You and I can both easily conceive a solution for Calebholiday’s design engineers. Obviously, real tank tracks actually have an arrangement of multiple wheels, and it would not be so difficult to have an arrangement that included some spring loaded tensioning wheels that could move around as required to maintain a constant tension throughout the system. But I am still not convinced that such an arrangement is really necessary, or that the differences in perception of the ground observer and the observer on board the tank are adequately explained by such a solution.
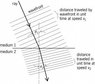
2. Distance traveled by the top track.
This is perhaps an even more basic point, but is something I have only realized in trying to work it out this time. The forward distance traveled by the top track at the speed calculated using the velocity addition formula is not just the appropriately contracted distance between the wheels. While the top track is traveling that distance, the tank itself is also traveling forward, thus the distance covered by any point on the top track is the appropriately contracted distance between the wheels, plus the appropriately contracted distance traveled by the tank in the time taken for that point to get from the rear wheel to the front wheel.
3. The equivalence to be proven
I was expecting to be able to show that velocities, distances and times balanced out in themselves. But they do not, so clearly that is not what is equivalent. My next thought was that it would be spacetime distance that was equivalent. So having arrived at values for velocity, length and time for each of the three cases, I envisaged plugging them into the good old Minkowski formula to find the distances in spacetime. But I can’t make that work either.
I know you say that you proved it in post #32. What you proved is that the number of segments per second gong forward are the same as the number of segments per second going rearward. I would have to stand with Austin0 and Calebholiday in saying that is not really a resolution of the apparent discrepancies of length and time.
In any case, I can anticipate that your patience has been exhausted. If so, let this post hang in the air for anyone else who cares to prod me in the direction of the solution I seek.