osiris40
- 1
- 1
Moved from a technical forum, so homework template missing
Hello, I'm trying to solve this, any idea please?
Basically: Demonstrate for the next three processes if the Time Series would be stationary, if not, it should establish the conditions for it to be stationary.
Thanks
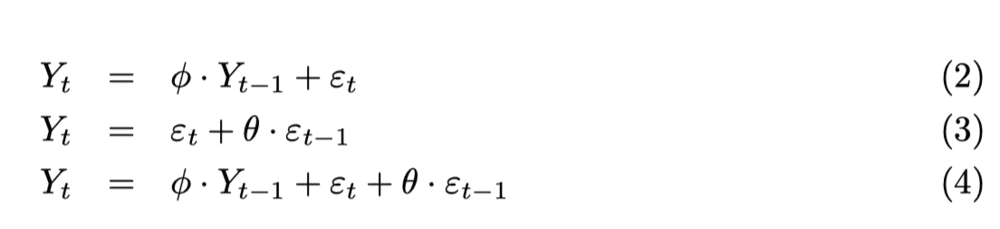
Basically: Demonstrate for the next three processes if the Time Series would be stationary, if not, it should establish the conditions for it to be stationary.
Thanks