- #1
DLawless
- 6
- 0
I am looking to understand how isoelectric point is defined and calculated. I read the paper "Isoelectric Point Calculator" (Kozlowski 2016) which gives the definition found everywhere 'isoelectric point pI is the pH value at which the net charge of a macromolecule is zero, and therefore its electrophoretic mobility is stopped'.
So far so good. But every recent paper I can find on the subject, like Kozlowski, goes on to mathematically define this as pH at which
$$\sum_{i=1}^n \frac{-1}{1+10^{pK_n-pH}} = \sum_{i=1}^n \frac{-1}{1+10^{pK_p-pH}}$$
which constitutes, apparently, the net charge or degree of ionization of the negatively-charged residues being equal to that of the positively-charged residues.
Curious as to the origin of this formula I found no explanation except that of Levene and Simms (1923: https://www.jbc.org/content/55/4/801.full.pdf). I quote their definition first
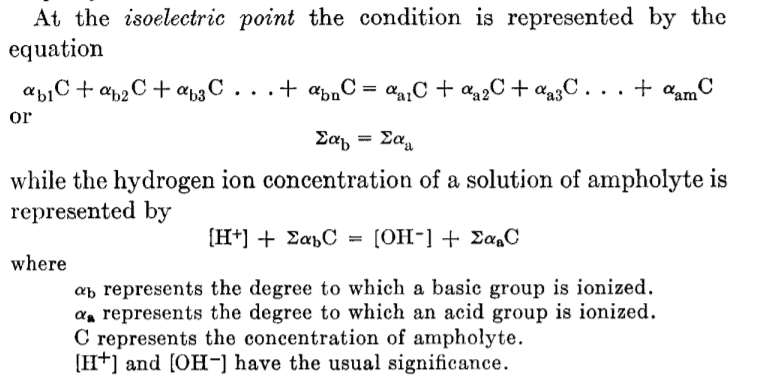
Then they say 'The following derivations of formulas for the calculation of isoelectric points are based on the assumption that the ionization of each group (acid or basic) takes place independently of the degree of ionization of other groups in the molecule.' On that basis they find it valid to write the isoelectric condition above as follows
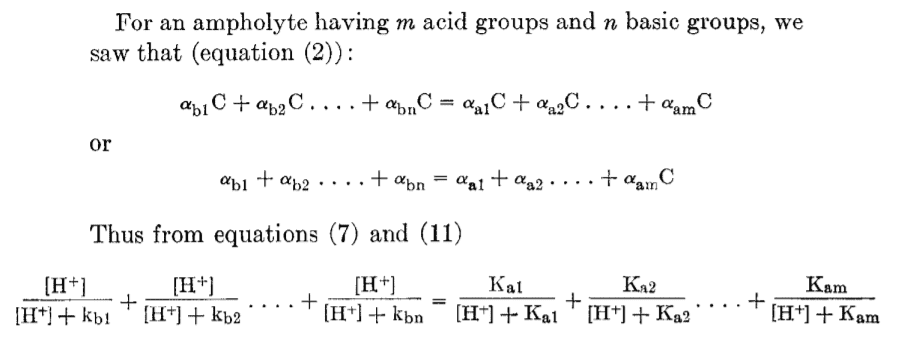
(7) and (11) are just the standard equations for degree of dissociation for monovalent positive (basic) and acidic (negative) components. This equation is obviously identical to the one from recent papers like Kozlowski.
I have two questions:
(1) If we are concerned about net charge, rather than net concentration, should we not be weighting by the charges on the forms? For example, consider a simple ampholyte like histidine (let's call it HX). Shouldn't the condition be 2 [H3X ^2+] + [H2X ^+] = [X ^-] rather than, as suggested above, [H3X ^2+] + [H2X ^+] = [X ^-]? As for example David Hitchcock did in his paper https://www.jbc.org/content/114/2/373.full.pdf (see p376)
(2) I am unclear that the form of the HH approximation is valid for matters of charge here. The sum of a single ampholyte's forms' degrees of ionization should not be going above 1. But here the left-hand side and right-hand side could each sum to (nearly) n and m respectively, as even a single term in the summations can approach 1. Thus I question whether the monovalent acid mixture thing is a reasonable approximation to summing up the degrees of ionization using the exact formulae from acid-base theory (i.e., the concentrations of each form from treating ampholyte as a single (n+m)-protic substance).
Am I missing something here in the mathematical derivation of the equation?
So far so good. But every recent paper I can find on the subject, like Kozlowski, goes on to mathematically define this as pH at which
$$\sum_{i=1}^n \frac{-1}{1+10^{pK_n-pH}} = \sum_{i=1}^n \frac{-1}{1+10^{pK_p-pH}}$$
which constitutes, apparently, the net charge or degree of ionization of the negatively-charged residues being equal to that of the positively-charged residues.
Curious as to the origin of this formula I found no explanation except that of Levene and Simms (1923: https://www.jbc.org/content/55/4/801.full.pdf). I quote their definition first
Then they say 'The following derivations of formulas for the calculation of isoelectric points are based on the assumption that the ionization of each group (acid or basic) takes place independently of the degree of ionization of other groups in the molecule.' On that basis they find it valid to write the isoelectric condition above as follows
(7) and (11) are just the standard equations for degree of dissociation for monovalent positive (basic) and acidic (negative) components. This equation is obviously identical to the one from recent papers like Kozlowski.
I have two questions:
(1) If we are concerned about net charge, rather than net concentration, should we not be weighting by the charges on the forms? For example, consider a simple ampholyte like histidine (let's call it HX). Shouldn't the condition be 2 [H3X ^2+] + [H2X ^+] = [X ^-] rather than, as suggested above, [H3X ^2+] + [H2X ^+] = [X ^-]? As for example David Hitchcock did in his paper https://www.jbc.org/content/114/2/373.full.pdf (see p376)
(2) I am unclear that the form of the HH approximation is valid for matters of charge here. The sum of a single ampholyte's forms' degrees of ionization should not be going above 1. But here the left-hand side and right-hand side could each sum to (nearly) n and m respectively, as even a single term in the summations can approach 1. Thus I question whether the monovalent acid mixture thing is a reasonable approximation to summing up the degrees of ionization using the exact formulae from acid-base theory (i.e., the concentrations of each form from treating ampholyte as a single (n+m)-protic substance).
Am I missing something here in the mathematical derivation of the equation?