USeptim
- 98
- 5
Hello,
Reading Richard Feynman’s book “Quantum Electrodynamics” (Edited by Advanced Book Classics), I read that the electron’s self-energy is infinite and that has been a trouble for QED during 20 years. Feynman proposed a solution based on a cut-off, but that’s not fully satisfactory and I think the question remains still opened.
The Feynman Diagram that describes self-energy is:
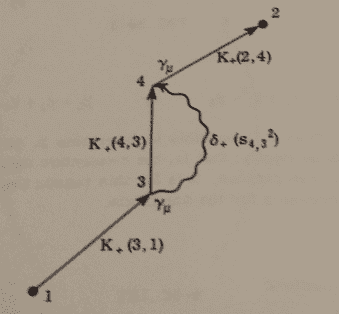
The integral used in the space-time dominion is:
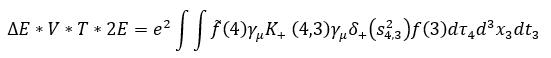
Where
· ΔE is the electron's self-energy
· V and T is the volume and the period of time and them both are infinite.
· The f's are the wave functions.
· K+ is the zeroth order propagator for a spinor using the Dirac equation.
· γμδ+(s24,3)γμ is the potential caused by point '3' over point '4'.
The integration is done over time and space in both points '3' and '4'. We can say that '3' emits a virtual photon and '4' absorbs it.
With this data, although we have to divide by 'V' and 'T' in order to obtain the self-energy, a divergent self-energy is obtained.
However, I think it's not correct to set the potential as γμδ+(s4,32)γμ since this expression is not taking into account the charge density of '3', |f(3)|2.
I think, another way to get the self-energy could be obtained by quantum mechanical means simply by:
ΔE = <f*(t4) |HSE| f(t4)>
Where HSE is the self-energy hamiltonian, that hamiltonian should be:
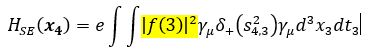
With this approach, the self-energy is no longer infinite, in fact for a plane-wave (dispersed over the infinite) it's zero.
Can anybody tell me where I am missed? Since for me looks clear that the self-energy should not be infinite.
Thanks a lot!
Sergio PratsNOTE: in self-interactions the initial and the final states must be the same, so this Hamiltonian must not have the same effect in the vawe-function that a normal Hamiltonian.
Reading Richard Feynman’s book “Quantum Electrodynamics” (Edited by Advanced Book Classics), I read that the electron’s self-energy is infinite and that has been a trouble for QED during 20 years. Feynman proposed a solution based on a cut-off, but that’s not fully satisfactory and I think the question remains still opened.
The Feynman Diagram that describes self-energy is:
The integral used in the space-time dominion is:
Where
· ΔE is the electron's self-energy
· V and T is the volume and the period of time and them both are infinite.
· The f's are the wave functions.
· K+ is the zeroth order propagator for a spinor using the Dirac equation.
· γμδ+(s24,3)γμ is the potential caused by point '3' over point '4'.
The integration is done over time and space in both points '3' and '4'. We can say that '3' emits a virtual photon and '4' absorbs it.
With this data, although we have to divide by 'V' and 'T' in order to obtain the self-energy, a divergent self-energy is obtained.
However, I think it's not correct to set the potential as γμδ+(s4,32)γμ since this expression is not taking into account the charge density of '3', |f(3)|2.
I think, another way to get the self-energy could be obtained by quantum mechanical means simply by:
ΔE = <f*(t4) |HSE| f(t4)>
Where HSE is the self-energy hamiltonian, that hamiltonian should be:
With this approach, the self-energy is no longer infinite, in fact for a plane-wave (dispersed over the infinite) it's zero.
Can anybody tell me where I am missed? Since for me looks clear that the self-energy should not be infinite.
Thanks a lot!
Sergio PratsNOTE: in self-interactions the initial and the final states must be the same, so this Hamiltonian must not have the same effect in the vawe-function that a normal Hamiltonian.