- #1
karush
Gold Member
MHB
- 3,269
- 5
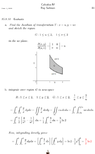
View attachment 8171
how do you graph this in Desmos ?
Assume the rest of the calculation is correct
much thank you ahead...
how do you graph this in Desmos ?
Assume the rest of the calculation is correct
much thank you ahead...