K+ Decay: Speculative or Feasible?

  • Thread starter Thread starter billbray
  • Start date Start date
  • Tags Tags
    Decay
billbray
Messages
24
Reaction score
0
Please see the attcahed image of K+ decay...

Question is - does anyone know how speculative this decay process is?? It just seems so far fetched.
 

Attachments

  • kaon.JPG
    kaon.JPG
    24.1 KB · Views: 538
Physics news on Phys.org
you can look it up in the particle data group booklet
 
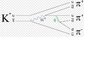
Yes, I saw it in the PDG mesons summary table, albeit without a feynman diagram. The feynman diagram shows everything between the up (at the top of the diagram) and the anti-up (at the bottom) comming from a w+ boson, half of it from a subsequent massive decay from a gluon. Being naive, it seems a bit much for nature to do.

My actual question is, does anyone know of any arlternative routes to this decay that have been proposed? All of my searches keep comming back to this one.

thanks
 
everything that is possible will occur if we wait long enough

recall that that is just one diagram in the full perturbation expansion of the scattering matrix, nature does not "calculate" decays with perturbation theory and feynman diagrams I think ;- )
 
What don't you like about this? why do you think it is "too much for nature to do"? (And remember, this only happens about 5% of the time)
 

Thread 'Toponium Discovered'

Toponium is a hadron which is the bound state of a valance top quark and a valance antitop quark. Oversimplified presentations often state that top quarks don't form hadrons, because they decay to bottom quarks extremely rapidly after they are created, leaving no time to form a hadron. And, the vast majority of the time, this is true. But, the lifetime of a top quark is only an average lifetime. Sometimes it decays faster and sometimes it decays slower. In the highly improbable case that...
View full post »

Thread 'Dirac-Delta from Normalization of Continuous Eigenfunctions'

I'm following this paper by Kitaev on SL(2,R) representations and I'm having a problem in the normalization of the continuous eigenfunctions (eqs. (67)-(70)), which satisfy \langle f_s | f_{s'} \rangle = \int_{0}^{1} \frac{2}{(1-u)^2} f_s(u)^* f_{s'}(u) \, du. \tag{67} The singular contribution of the integral arises at the endpoint u=1 of the integral, and in the limit u \to 1, the function f_s(u) takes on the form f_s(u) \approx a_s (1-u)^{1/2 + i s} + a_s^* (1-u)^{1/2 - i s}. \tag{70}...
View full post »

Similar threads

A Decay Modes of J/psi: Understanding Gamma and Hadron Decays
Replies
2
Views
2K
B Where does the mass of a W boson come from in beta decay?
Replies
3
Views
3K
A Beta/gamma decay probabilities
Replies
2
Views
2K
A Pandora's Box: Carbon-14 vicious cycle from transmutation
Replies
1
Views
3K
A Creating a new compound (involving K,Ca,H,N). Is it possible?
Replies
1
Views
1K
A How Does the ss¯ Pair Affect the Partial Width Γ2 in Gluon Decays?
Replies
4
Views
3K
I How Does Beta Decay Relate to the Role of W Bosons in Weak Nuclear Force?
Replies
4
Views
4K
I Estimating decay yields from fits to these distributions
Replies
2
Views
2K
I Energy reduction/deflection of beta particles due to isotope geometry
Replies
2
Views
2K
I ATLAS and CMS see signs of Higgs->muons decay
Replies
17
Views
6K

Hot Threads

Recent Insights

Back
Top