K-th Prime Proofs & Co-Prime Numbers

In summary, the conversation discusses two problems related to the k-th prime and co-primes. The first problem involves proving a statement involving pk, the k-th prime, and determining whether the number on the right is prime or composite and its factors. The second problem is whether there is a set of four coprime numbers that cannot be grouped into sets of three. The conversation ends with a clarification that the expression being discussed is p_{k+1} \leq (p_1~p_2 \cdots p_k)+1.
  • #1
vmx200
2
0
I am having a hard time making head way on two problems related to the k-th prime and one about co-primes that I would really appreciate some help and/or direction!

Prove that:
(let pk be the k-th prime)
Picture1-1.png


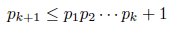
and

Picture3-2.png

Regarding co-primes... is there any way to find a set of four numbers that are coprime, but cannot be subsequently grouped into sets of three that are?

Again, thank you for your time and generosity in helping me out!
 
Last edited:
Physics news on Phys.org
  • #2
In the first problem, is the number on the right prime or composite? If it's composite, what can you say about its factors?
 
  • #3
hamster143 said:
In the first problem, is the number on the right prime or composite? If it's composite, what can you say about its factors?

Oh, sorry!
Uhmn... pk is the k-th prime, so pk + 1 (the right most term) would be a composite, I believe?
 
  • #4
I'm asking about the whole thing: 1 + the product of all primes up to pk.
 
  • #5
vmx200 said:
Oh, sorry!
Uhmn... pk is the k-th prime, so pk + 1 (the right most term) would be a composite, I believe?
I believe you are misreading the expression.

To clarify: [itex]p_{k+1} \leq (p_1~p_2 \cdots p_k)+1[/itex]
 

FAQ: K-th Prime Proofs & Co-Prime Numbers

What is a K-th prime proof?

A K-th prime proof is a mathematical proof that verifies the primality of the K-th prime number. This means that the proof shows that the K-th prime number is only divisible by 1 and itself.

How is a K-th prime proof different from a regular prime proof?

A K-th prime proof is specifically focused on verifying the primality of the K-th prime number, while a regular prime proof can be used for any prime number. K-th prime proofs are often more complex and require more advanced mathematical techniques.

What are co-prime numbers?

Co-prime numbers are two numbers that do not have any common factors other than 1. In other words, their greatest common divisor (GCD) is 1. For example, 8 and 9 are co-prime numbers because their GCD is 1, while 6 and 8 are not co-prime because their GCD is 2.

How are K-th prime proofs and co-prime numbers related?

K-th prime proofs and co-prime numbers are related because they both involve the properties of prime numbers. Co-prime numbers are often used in K-th prime proofs as a way to show that the K-th prime number is not divisible by any other numbers, except for 1 and itself.

Why are K-th prime proofs important?

K-th prime proofs are important because they help to verify the primality of prime numbers, which are crucial in many areas of mathematics and science. They also help to advance our understanding of number theory and can lead to the discovery of new patterns and relationships between prime numbers.

Similar threads

I Fundamental theorem of arithmetic from Jordan-Hölder theorem
Replies
5
Views
371
I How to Prove a Congruence Relation for Prime Numbers?
Replies
17
Views
2K
I Can This Formula Identify All Prime Numbers?
Replies
2
Views
1K
Proof about a prime between k and 2k.
Replies
6
Views
5K
Determine (with proof) the set of all prime numbers
Replies
3
Views
1K
What is the fastest algorithm for finding large prime numbers?
Replies
14
Views
2K
Primary Ideals, prime ideals and maximal ideals.
Replies
1
Views
2K
Can m(m+1) Equal kn for Natural Numbers m, k, and n?
Replies
16
Views
5K
MHB Primary Ideals, prime ideals and maximal ideals.
Replies
1
Views
3K
Proving (a weaker form of) Bertrand's postulate
Replies
7
Views
5K

Hot Threads

Recent Insights

Back
Top