Kinetic and Potential Energy Question

[student34]

Homework Statement

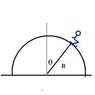
A skier starts skiing from the very top of a frictionless sphere of ice with very little initial speed. At what angle from the the vertical will the skier leave the sphere of ice?

Homework Equations

This question was in the Kinetic and Potential Energy chapter, so I guess we are suppose to use the kinetic and potential energy equations K = (1/2)*m*v^2, U = m*g*y and E = K + U.

The Attempt at a Solution

I can't even attempt this because I don't know how to relate the two energies in a way that would give me the answer.

This question is so much more different than any other question in the chapter.

 

[ehild]

Apply conservation of energy. What is the KE at the top? What is the KE and PE on the surface at height h deeper then the top? How is the height related to the angle from the vertical?
What force keeps the skier on the circular track?


ehild

 

[Sunil Simha]

The skier will stop moving on the sphere once the centrifugal force is exactly canceled by the component of weight along the radius of the sphere.

 

[student34]

Apply conservation of energy. What is the KE at the top? What is the KE and PE on the surface at height h deeper then the top? How is the height related to the angle from the vertical?
What force keeps the skier on the circular track?


ehild

F(gravity) = m*g*cosθ
F(centripetal) = (m*v^2)/r
(1/2)*m*v^2 = m*g*h, where h = r*cos and v = (2*r*g*cosθ)^(1/2)
But when I make Fg = Fc, I get 2*g*cosθ = g*cosθ which comes to 2 = 1.

 

[ehild]

F(gravity) = m*g*cosθ
F(centripetal) = (m*v^2)/r
(1/2)*m*v^2 = m*g*h, where h = r*cos and v = (2*r*g*cosθ)^(1/2)
But when I make Fg = Fc, I get 2*g*cosθ = g*cosθ which comes to 2 = 1.

You made a mistake in the equation for conservation of energy.

The energy at the top of the hill is equal to the energy at the point where the skier detaches from the hill.
What is the potential energy at the top? What is it at the point of detach?

ehild

 

[student34]

You made a mistake in the equation for conservation of energy.

Hmmm, I can't find the mistake. Doesn't initial potential energy equal final kinetic energy?

The energy at the top of the hill is equal to the energy at the point where the skier detaches from the hill.
What is the potential energy at the top? What is it at the point of detach?

ehild

Oh boy, that seems to be my wall. I have to give up. I have spent way too much time on this question.

 

[student34]

Can somebody please give me the answer. The answer will hopefully help me because I just can't make the connection myself.

 

[ehild]

Hmmm, I can't find the mistake. Doesn't initial potential energy equal final kinetic energy?

No. The initial KE+initial PE is equal to the final KE +final PE



ehild

 

[student34]

No. The initial KE+initial PE is equal to the final KE +final PE



ehild

Am I on the right track by making F(normal) = F(gravity)?

 

[Sunil Simha]

Am I on the right track by making F(normal) = F(gravity)?

By F(normal) if you mean the normal reaction and F(gravity) as mgcosθ, then yes. You have only committed a mistake on post #4 in the equation of the energy as ehlid has pointed out..

 

[student34]

By F(normal) if you mean the normal reaction and F(gravity) as mgcosθ, then yes. You have only committed a mistake on post #4 in the equation of the energy as ehlid has pointed out..

I should have been more specific because I do know that EP(initial) = EK(final). Knowing that and knowing all of the hints posted in this forum, I still don't even know where to start when trying to answer this question.

 

[ehild]

I should have been more specific because I do know that EP(initial) = EK(final). Knowing that and knowing all of the hints posted in this forum, I still don't even know where to start when trying to answer this question.

You know it wrong.

ehild

 

[student34]

You know it wrong.

ehild

My book says K1 + U1(gravity) = K2 + U2(gravity) where 1 means initial and 2 means final. In this situation I have K1 = 0 and U2(gravity) = 0, so doesn't U1 = K2?

 

[ehild]

You said that U=mgh, and h= Rcosθ. Is it zero at the final position?KE is equal to the potential difference between the initial and final positions.

ehild

 

[student34]

You said that U=mgh, and h= Rcosθ. Is it zero at the final position?KE is equal to the potential difference between the initial and final positions.

ehild

I see. But I still cannot see how this can give us the where the skier leaves the surface of the ice ball. I feel like I am close by choosing F(gravity) to equal F(reaction to Fc), but I just can't go further.

When I tried in Post #4, I ended up with 2 = 1.

 

[Sunil Simha]

Go back to the basics. What was the initial potential energy? What will be the final potential energy?
What then, will be the potential energy difference?

 

[student34]

Go back to the basics. What was the initial potential energy? What will be the final potential energy?
What then, will be the potential energy difference?

I think y*m*g = y2*m*g + (1/2)*m*v2^2

 

[Doc Al]

F(gravity) = m*g*cosθ
F(centripetal) = (m*v^2)/r
(1/2)*m*v^2 = m*g*h, where h = r*cos and v = (2*r*g*cosθ)^(1/2)
But when I make Fg = Fc, I get 2*g*cosθ = g*cosθ which comes to 2 = 1.

Your mistake is here: h = r*cosθ

What you're trying to do is ΔKE = mgΔh, but you must correctly express Δh in terms of r and θ. Then you'll be fine.

 

[student34]

Your mistake is here: h = r*cosθ

What you're trying to do is ΔKE = mgΔh, but you must correctly express Δh in terms of r and θ. Then you'll be fine.

Thanks, I get it now.