Roze
- 14
- 0
Homework Statement
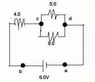
Find the currents in the circuit shown in the figure attached.
Homework Equations
I actually have the solution worked out but I don't understand why something was done. So they chose to travel the bottom loop and the top loop clockwise in both cases. So they set up the equation:
sum deltaV = Vbattery + V4.0 + V9.0
What I don't understand is why they chose to add the V9.0, rather than the V5.0, or both. How do I know that this is the resistor you use for this equation? I understand you're traveling the loop clockwise, but I don't understand why the 9.0 resistor is used rather than the 5.0 or their equivalent resistance.
Also, when they plug in the numbers for this equation they give:
sum deltaV = 6.0V -4.0I2 - 9.0I3
Why are the 4.0 and 9.0 components negative? Is it because they're on the other side of the battery?
Similarly, for the top loop they give the equation:
sum deltaV = -5.0I2 + 9.0I3
Why in this case is the 5.0 negative but the 9.0 positive?
The Attempt at a Solution
See above.
Apologies for the terrible picture.