Niall Kennedy
- 7
- 0
Member advised to use the homework template for posts in the homework sections of PF.
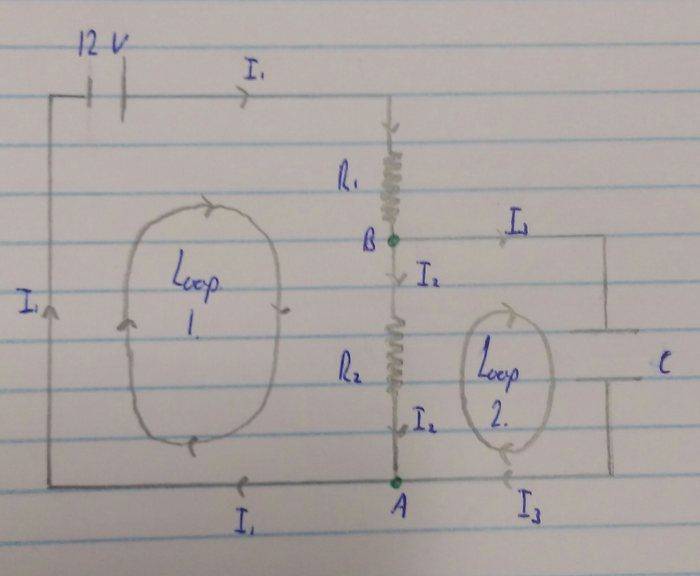
A 5μF capacitor is connected in parallel with a 2MΩ resistor and the combination is then connected in series with a 1MΩ resistor through a switch to a 12V battery. Find the time taken for the voltage across the capacitor to rise from zero initial value to 2V after the switch is closed.From what I understand this requires Kirchoff's loop and junction rules which is okay up until I hit the voltage across the capacitor which is where I get stuck.Here's the diagram I made to work from, hopefully it's right: