Kramers-Kronig relation for refractive index

[Another]

I don't understand why sometime

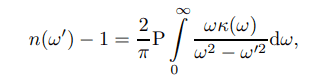for paper : Kramers-Kronig relations and sum rules of negative refractive index media

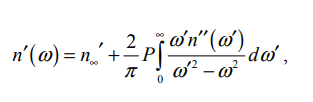for paper : A Differential Form of the Kramers-Kronig Relation for Determining a Lorentz-Type of Refractive Index*

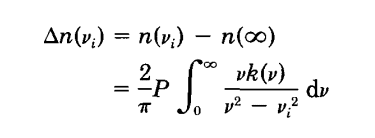for paper : Comparison Among Several Numerical Integration Methods for Kramers-Kronig Transformation

I know maybe $\omega = \nu$

What different between $Δn(\omega)$, $n(\omega) - 1$ and $n(\omega)-n_{∞}$

 

[vanhees71]

Where is this from?

The formulae given are all socalled "subtracted dispersion relations". It's making use of the spectral theorem aka. Kramers-Kronig relations which are very general relations resulting from retarded Green's functions and causality.

The retardation condition for a Green's function means that it's Fourier transform wrt. time leads to a function that is analytic in the upper complex frequency half-plane and from this you can derive the relations between real and imaginary part of $\tilde{G}_{\text{ret}}(\omega)$.

If you have a function, for which the integral is not convergent, because the imaginary part doesn't vanish at infinity quickly enough you can derive subtracted dispersion relations. In your example that's applied to the refractive index, which usually goes to a constant for $\omega \rightarrow \infty$. In this case of the refractive index (though I'm a bit puzzled, because the KK relations refer to $\epsilon(\omega)$ rather than $n(\omega)$).