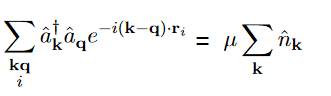SUMMARY
The discussion centers on the application of the Kronecker delta in the context of creation and annihilation operators, specifically addressing the expression involving the sum over index i and its relation to the Kronecker delta. Participants clarify that the sum over i refers to the subscript associated with r, while the Kronecker delta simplifies the exponential term, effectively eliminating the need for the sum over i. The conversation highlights the importance of understanding the notation and the implications of the Kronecker delta in quantum mechanics.
PREREQUISITES
- Understanding of Kronecker delta notation in mathematics
- Familiarity with creation and annihilation operators in quantum mechanics
- Basic knowledge of discrete Fourier transforms
- Concept of complex exponentials in physics
NEXT STEPS
- Study the properties and applications of the Kronecker delta in quantum mechanics
- Explore the role of creation and annihilation operators in quantum field theory
- Learn about discrete Fourier transforms and their significance in physics
- Investigate the implications of complex exponentials in wave functions
USEFUL FOR
Physicists, quantum mechanics students, and anyone studying the mathematical foundations of quantum field theory will benefit from this discussion.