cvali
- 1
- 0
Hi, I'm a student working with my group to create a lab for our final lab project. Me and my teammates are stuck on how we should begin to set up the project. I attached 4 photos, one of the pendulum setup, one of the model of our pendulum setup, and two others of the lab sheet guide.
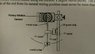
The purpose of the lab project is to design and build a physical pendulum with the smallest possible period. The physical pendulum must be built of the supplied metal tube, metal collar, two TT spools, white TT rod, and 10-gram disk. It must be mounted on the supplied rotary motion sensor using the encoder's largest radius pulley. The angular displacement of the rod from its natural resting position must never be more than 10 degrees.
In the pendulum setup (referring to the model), the only thing we can manipulate is the TT spools/rod and Metal collar, everything else must stay the same.
In terms of the first section of the project, image IMAG0075. we were thinking the following with respect to the chart (though this can be altered if necessary):
1) Neglect
2) Solid Cylinder
3) Annular Cylinder
4) Annular Cylinder
5) Solid Cylinder
6) Annular Cylinder
We're stuck on the setup of the mathematical expression we are to derive to solve for Tminimum from the information given. We must include the pendulums period (Ttheory) in terms of d1 and d2 (d1 and d2 being distances from the rods axis of rotation to the center of the mass of the TT spool and the center of mass of the metal collar).
We believe we should be using the following (inertia) equations in respect to image IMAG0075
1) n/a
2) (1/12)ML^2
3) MR^2
4) MR^2
5) (1/12)ML^2
6) MR^2
We're not sure if we are on the right track. Any advice on how we should approach this would be awesome, or an explanation on how we should put the formulas together to attain the lowest period in which the lowest point of the pendulum swings.
2. Relevant
The purpose of the lab project is to design and build a physical pendulum with the smallest possible period. The physical pendulum must be built of the supplied metal tube, metal collar, two TT spools, white TT rod, and 10-gram disk. It must be mounted on the supplied rotary motion sensor using the encoder's largest radius pulley. The angular displacement of the rod from its natural resting position must never be more than 10 degrees.
In the pendulum setup (referring to the model), the only thing we can manipulate is the TT spools/rod and Metal collar, everything else must stay the same.
In terms of the first section of the project, image IMAG0075. we were thinking the following with respect to the chart (though this can be altered if necessary):
1) Neglect
2) Solid Cylinder
3) Annular Cylinder
4) Annular Cylinder
5) Solid Cylinder
6) Annular Cylinder
We're stuck on the setup of the mathematical expression we are to derive to solve for Tminimum from the information given. We must include the pendulums period (Ttheory) in terms of d1 and d2 (d1 and d2 being distances from the rods axis of rotation to the center of the mass of the TT spool and the center of mass of the metal collar).
We believe we should be using the following (inertia) equations in respect to image IMAG0075
1) n/a
2) (1/12)ML^2
3) MR^2
4) MR^2
5) (1/12)ML^2
6) MR^2
We're not sure if we are on the right track. Any advice on how we should approach this would be awesome, or an explanation on how we should put the formulas together to attain the lowest period in which the lowest point of the pendulum swings.
Homework Statement
2. Relevant