Yoonique
- 105
- 0
1. Homework Statement
A ladder on the rough floor is leaning against a vertical rough wall. The ladder has length l and mass m. The coefficients of friction are μ for both contact surfaces. What is the smallest angle between the ladder and the floor?
∑F=ma
∑τ = F⊥ r
fs ≤ μsN
[/B]
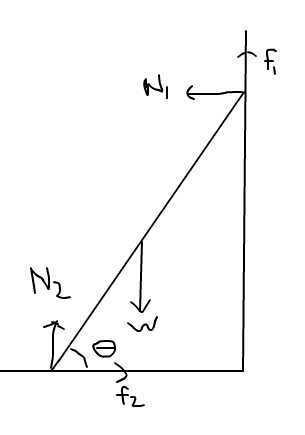
∑Fy = 0
N2 + f1 - W = 0
∑Fx = 0
f2 - N1 = 0
f2 = N1
∑τ about the ground = 0
N1lsinθ + f1lcosθ - W(l/2)(cosθ) = 0
For θ to be the smallest angle, what is the condition? Is it f1 = μN1 or f2 = μN2 or both of them need to happen at the same time?
A ladder on the rough floor is leaning against a vertical rough wall. The ladder has length l and mass m. The coefficients of friction are μ for both contact surfaces. What is the smallest angle between the ladder and the floor?
Homework Equations
∑F=ma
∑τ = F⊥ r
fs ≤ μsN
The Attempt at a Solution
[/B]
∑Fy = 0
N2 + f1 - W = 0
∑Fx = 0
f2 - N1 = 0
f2 = N1
∑τ about the ground = 0
N1lsinθ + f1lcosθ - W(l/2)(cosθ) = 0
For θ to be the smallest angle, what is the condition? Is it f1 = μN1 or f2 = μN2 or both of them need to happen at the same time?
Last edited:
