hanyas
- 7
- 0
I'm trying to write down the equations of motion for a tetherball moving in 3D around a pole while the string is getting shorter.I've started with lagrange equations:
<br /> x(t)=l(t) \sin (\theta) \cos (\phi)\\<br /> y(t)=l(t) \sin (\theta) \sin (\phi)\\<br /> z(t)=h(t)+l(t) \cos(\theta)\\ \\<br /> <br /> T = \frac{1}{2}m(\dot x^2 +\dot y^2+\dot z^2)\\<br /> U=m g l(t)(1-\cos(\theta)) + mg(S-(h(t)+l(t))) <br />
where l(t) is the length of the string. Here only I am assuming the radius of the pole is really small compared to l. The polar angle is \theta(t). h(t) is the change in height due to the string wrapping on the pole. S is the length of string when unwrapped.
The change in length along is given by:
<br /> \dot l(t) = -\frac{r\dot\phi}{ \sin(\theta)}<br />
where r is the radius of the pole. And the sliding pivot point is given by:
<br /> \dot h(t) = \frac{r\dot\phi}{ \tan(\theta)}<br />
After plugging those in T I apply the Lagrange derivative to L = T-U and solve for \ddot \theta and \ddot \phi
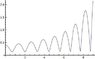
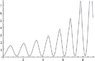
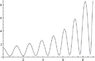
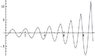
Now when I simulate the results I get a linear velocity that is some how increasing which is not supposed to happen for a tetherball because no new energy has been introduced to the system and the angular momentum is not conserved.
I would appreciate some feedback
<br /> x(t)=l(t) \sin (\theta) \cos (\phi)\\<br /> y(t)=l(t) \sin (\theta) \sin (\phi)\\<br /> z(t)=h(t)+l(t) \cos(\theta)\\ \\<br /> <br /> T = \frac{1}{2}m(\dot x^2 +\dot y^2+\dot z^2)\\<br /> U=m g l(t)(1-\cos(\theta)) + mg(S-(h(t)+l(t))) <br />
where l(t) is the length of the string. Here only I am assuming the radius of the pole is really small compared to l. The polar angle is \theta(t). h(t) is the change in height due to the string wrapping on the pole. S is the length of string when unwrapped.
The change in length along is given by:
<br /> \dot l(t) = -\frac{r\dot\phi}{ \sin(\theta)}<br />
where r is the radius of the pole. And the sliding pivot point is given by:
<br /> \dot h(t) = \frac{r\dot\phi}{ \tan(\theta)}<br />
After plugging those in T I apply the Lagrange derivative to L = T-U and solve for \ddot \theta and \ddot \phi
Now when I simulate the results I get a linear velocity that is some how increasing which is not supposed to happen for a tetherball because no new energy has been introduced to the system and the angular momentum is not conserved.
I would appreciate some feedback
Last edited:


 )
)