Lagrangian of conic pendulum-rod

[Hanuda]

Homework Statement

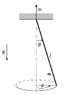
So, basically there is a stick, mass m and length l, that is pivoted at its top end, and swings around the vertical axis with angular frequency omega. The stick always makes an angle theta with the direction of gravity. I am told there are 2 degrees of freedom (theta, phi), with phi being the angle around the 'equator' (see attached picture). Phi-dot=omega.

a) Determine the kinetic energy and show that it is given by a function of the type T(phi-dot, theta-dot, theta).

The attempt at a solution

I assume I am supposed to use spherical coordinates for theta and phi, so it should look something like:

T=\frac{1}{2}m(\dot r^2 + r^2\dot \theta^2 + r^2sin^2(\theta)(\dot \phi)^2)

But we know that the kinetic energy of the pendulum only depends on theta, theta-dot, and phi-dot. So how should it look?

Thanks for your help.

 

[BvU]

What is the meaning of your r ?