leopard
- 123
- 0
How can I transform
F(s) = \frac{1}{(s-2)^2}
?
I cannot see that any of the functions in my table is useful...
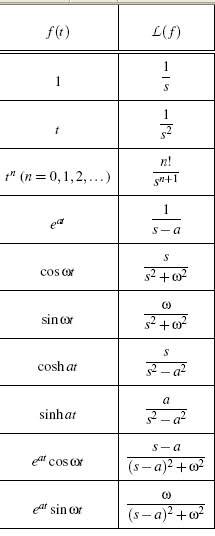
F(s) = \frac{1}{(s-2)^2}
?
I cannot see that any of the functions in my table is useful...