Launching a ball with a flywheel design into a goal

[HeyAwesomePeopl]

Hello all,

My robotics club at school will be entering the VEX Nothing But Net competition. We are beginning to design the robot and it's launcher specifically.

We want our flywheel design to be two wheels on each side, on a horizontal line like this. We would squeeze the balls between the wheels at a certain speed to launch the balls to the goal.

This is our goal

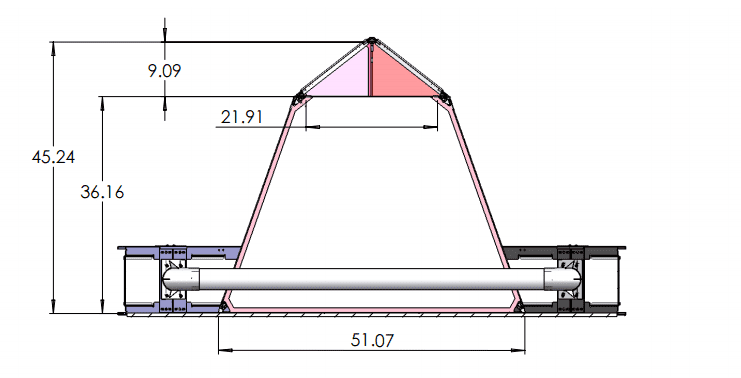
and our playing field

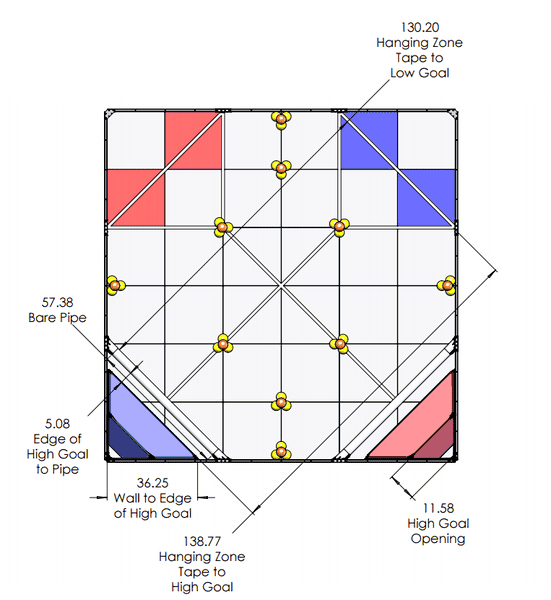
So right away I want to calculate the exact location I want the ball to land. Obviously, this would be in the middle of the high goal zone.

This seems like a simple calculation. At first to find it I was just using the pythagorean theorem, but then I realize that our robot won't be placed in a corner. It will be placed on one of the red/blue squares. Already this means I have to do more math. I figured the launcher would be in the middle of the square, resulting in the middle of the goal being about a 98.93inch linear line away(this number includes the pythagorean theorem for the height of the goal, otherwise it would just be 89.1 inches as a flat line across the field)

That is my first question, how accurate is my math?

My second question is a lot more complicated. I need to figure out how fast I need to spin my flywheels in order to launch the balls where I want them. How do I do this?

Using an online launch velocity calculator, I am getting that to shoot 98.93 inches, that at an angle of 45 degrees I would need the launch velocity to be 4.9616... m/s. This just doesn't seem right, but if it is, then how would I figure out what the launch velocity of the ball will be through the flywheel based on how fast the flywheel is spinning and how much space there is between the wheels(how much it squeezes the ball)

This is all new to me so sorry if I don't understand something

Thanks,
HeyAwesomePeople

 

[mfb]

I'm not sure if I understand the geometry. Do you have to consider the shape of the playing field, or can you reduce it to a simple 2 D problem (height + width)? Horizontal velocity will stay constant (neglecting air resistance), vertical velocity will change with downwards acceleration from gravity. The typical introductory mechanics problem with solutions in every textbook.