Law of conservation of angular momentum

[Boltzman Oscillation]

Given the figure, how can i arrive to this formula knowing that angular momentum is conserved?

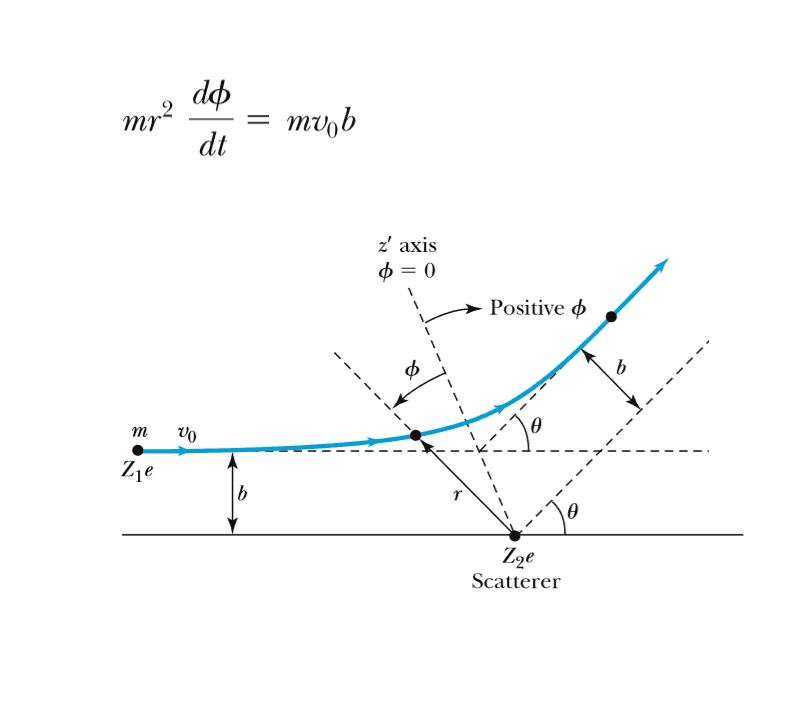
I know that p = mv and L = p x r. So the initial momentum will be L1 = mV x R and the final momentum will be L2 = mv x r.

I am not sure how R will equal to b since the distance between the initial position of the electron is clearly not b distance apart from the scatterer. I am also not sure how to modify the final angular momentum to fit the formula.

 

[A.T.]

I know that p = mv and L = p x r. So the initial momentum will be L1 = mV x R and the final momentum will be L2 = mv x r.

I am not sure how R will equal to b since the distance between the initial position of the electron is clearly not b ...

Your b is the magnitude of the r vector component, that is perpendicular to p (or v), before and after the scattering. Do you understand the cross product?
https://en.wikipedia.org/wiki/Cross_product

 

[Boltzman Oscillation]

Your b is the magnitude of the r vector component, that is perpendicular to p (or v), before and after the scattering. Do you understand the cross product?
https://en.wikipedia.org/wiki/Cross_product

yes I understand the cross product but I've not had enough practice with it (my math foundations class was a mess). Isnt the magnitude how large the arrow is? In that case then the magnitude b wouldn't be the same as the magnitude of vector r would it? r stretches and shortens throughout the path of movement.

 

[A.T.]

In that case then the magnitude b wouldn't be the same as the magnitude of vector r would it?

Look at your picture. Do they look the same?

r stretches and shortens throughout the path of movement.

Yes, but b is just one component of r, before and after scattering, not throughout.

 

[Boltzman Oscillation]

Look at your picture. Do they look the same?Yes, but b is just one component of r, before and after scattering, not throughout.

ohh so I am only looking at before and after the scattering and not throughout. Hmm so in that case r = b in both cases. Now the velocity of the particle after the scattering can be described by position/time. Well position will be given by the angle. The derivative of position in respect to time is position right? So the velocity will equal d(angle)/dt. The final angular momentum will then equal:

L = m * d(angle)/dt x b. = m*(dΦ/dt)*bsin(90) = m*(dΦ/dt)?

Ugh why dint I learn vector calculus correctly? :(
I guess its best to take my time to learn it now so it won't impede me later.

 

[A.T.]

b is just one component of r

r = b

No, see above.

 

[Boltzman Oscillation]

No, see above.

Okay so L = m*(dΦ/dt) x r = m*(dΦ/dt)*b*sin(angle between the two) ?

 

[A.T.]

Okay so L = m*(dΦ/dt) x r = m*(dΦ/dt)*b*sin(angle between the two) ?

Which is greater, b or |r|?

 

[Boltzman Oscillation]

Which is greater, b or |r|?

err I thought b was the magnitude of r? so arent they the same in errrr greatness?

 

[Boltzman Oscillation]

err I thought b was the magnitude of r? so arent they the same in errrr greatness?

sigh, on the initial momentum then b will be the yth component of r while in the final momentum r will be greater than b.

 

[A.T.]

sigh, on the initial momentum then b will be the yth component of r while in the final momentum r will be greater than b.

So what is the mathematical relation between b and r?

 

[Boltzman Oscillation]

So what is the mathematical relation between b and r?

Well for initial momentum:

sin(θ) = b/r

I guess for the final momentum this doesn't change. On inspection of the figure, I conclude that it doesn't change. Thus b = rsin(θ).
Thus L = m*(dΦ/dt) x r = m*(dΦ/dt)*b*sin(θ) = m*(dΦ/dt)*b^2/r?