grace77
- 43
- 0
Problem statement
What is the left hand and right hand limit of 1/x^2 -4 at its vertical asymptote?
Revelant equations
None
Attempt at a solution
It's vertical asymptote are 2 and -2.
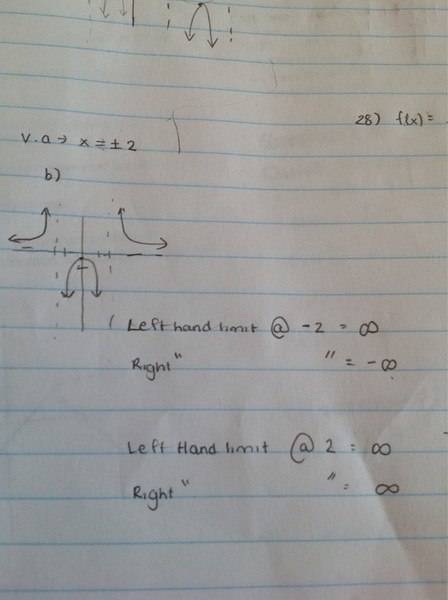
I have attached my work . I understand it however at the back of the book it says the left hand limit at 2 is negative infinity. That I don't understand as if you look at the graph I have drawn the left hand limit at 2 is going in a positive direction.
Does anyone have any insight on this? Thank you!
What is the left hand and right hand limit of 1/x^2 -4 at its vertical asymptote?
Revelant equations
None
Attempt at a solution
It's vertical asymptote are 2 and -2.
I have attached my work . I understand it however at the back of the book it says the left hand limit at 2 is negative infinity. That I don't understand as if you look at the graph I have drawn the left hand limit at 2 is going in a positive direction.
Does anyone have any insight on this? Thank you!