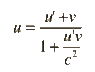weirdobomb
- 15
- 0
10. The average lifetime of a pi meson in its own frame of reference is 2.6 x 10^-8 s. If the meson
moves with a speed of 0.95c, what is (a) its mean lifetime as measured by an observer on Earth and
(b) the average distance it travels before decaying, as measured by an observer
on Earth?
(a) using the formula for time dilation
mean lifetime measured on Earth I found t = 8.12 x 10^-4 s
(b) I calculated the distance traveled in the particle to travel in its own frame L = 7.44 m
I took that value and used the formula for length contraction
average distance traveled measured on Earth before decaying L = 23.8 m.
I am pretty sure my answers are correct, or at least the concept is. My question is for (b), how do I find the velocity of the particle measured on Earth? What I want to do is take the Earth measured velocity to multiple by the answer from (a) to have a different way to answer (b).
I think I have to use the velocity formula in the attachment but doesn't that one require the particle to be moving in an already moving frame (v=velocity of frame u'=particle velocity in that frame).
moves with a speed of 0.95c, what is (a) its mean lifetime as measured by an observer on Earth and
(b) the average distance it travels before decaying, as measured by an observer
on Earth?
(a) using the formula for time dilation
mean lifetime measured on Earth I found t = 8.12 x 10^-4 s
(b) I calculated the distance traveled in the particle to travel in its own frame L = 7.44 m
I took that value and used the formula for length contraction
average distance traveled measured on Earth before decaying L = 23.8 m.
I am pretty sure my answers are correct, or at least the concept is. My question is for (b), how do I find the velocity of the particle measured on Earth? What I want to do is take the Earth measured velocity to multiple by the answer from (a) to have a different way to answer (b).
I think I have to use the velocity formula in the attachment but doesn't that one require the particle to be moving in an already moving frame (v=velocity of frame u'=particle velocity in that frame).
Attachments
Last edited: