pujam3
- 4
- 0
Homework Statement
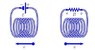
Two coils are suspended around a central axis as shown in the figure below. One coil is connected to a resistor with ends labeled a and b. The other coil is connected to a battery E The coils are moving relative to each other as indicated by the velocity vectors v. Use Lenz’s law to answer the following question concerning the direction of induced currents and magnetic fields.
1)The direction of the magnetic field in the coil with the battery attached is
A1: from right to left (\Leftarrow Bprimary).
A2: from left to right (Bprimary \Rightarrow).
2)The direction of the induced magnetic field in the coil with the resistor attached is
B1: from right to left (\Leftarrow Binduced).
B2: from left to right (Binduced \Rightarrow).
3)The direction of the induced current in resistor R is
C1: from b through R to a (\leftarrowI).
C2: from a through R to b (I\rightarrow).
Picture is attached.
1. A1, B1, C1 (<-- my guess, but incorrect)
2. A2, B1, C1
3. A1, B2, C1
4. A1, B2, C2
5. A2, B2, C1
6. A1, B1, C2
7. A2, B2, C2
8. A2, B1, C2
Homework Equations
None
The Attempt at a Solution
1) The coil with the battery, the current flows from + to -, and I have made the conclusion that the magnetic field goes from right to left since in a coil the current flows 'downwards' into the coil at the South pole of the field, and the current flows 'upward' out of the coil at the North pole of the field. I'm not sure if my speculation is correct though.
2) If what i said in question 1 is correct, then i can make the left end of the coil with the battery the "north pole" and the right end of the battery the "south pole". As the coils are moving away from each other, the induced magnetic field in the coil with the resistor attached would be towards the coil with the battery (right to left) as the (3) current should flow counterclockwise in the coil with the resistor (from b to a)
Apparently I'm making a mistake somewhere here as my answer was not correct.