Edgar53
- 3
- 0
The 4-Squares-Identity of Leonhard Euler
(https://en.wikipedia.org/wiki/Euler%27s_four-square_identity) :
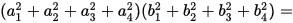
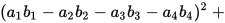
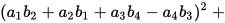
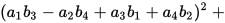
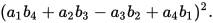
has the numeric structure of Maxwell’s equations in 4-space:
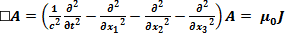
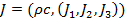
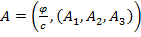
Is somebody aware of litterature about this?
(https://en.wikipedia.org/wiki/Euler%27s_four-square_identity) :
has the numeric structure of Maxwell’s equations in 4-space:
Is somebody aware of litterature about this?
Attachments
-
 upload_2017-11-19_23-4-30.jpg2.4 KB · Views: 847
upload_2017-11-19_23-4-30.jpg2.4 KB · Views: 847 -
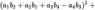 upload_2017-11-19_23-4-30.jpg1.7 KB · Views: 868
upload_2017-11-19_23-4-30.jpg1.7 KB · Views: 868 -
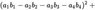 upload_2017-11-19_23-4-30.jpg1.6 KB · Views: 910
upload_2017-11-19_23-4-30.jpg1.6 KB · Views: 910 -
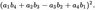 upload_2017-11-19_23-4-30.jpg1.7 KB · Views: 399
upload_2017-11-19_23-4-30.jpg1.7 KB · Views: 399 -
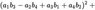 upload_2017-11-19_23-4-30.jpg1.7 KB · Views: 462
upload_2017-11-19_23-4-30.jpg1.7 KB · Views: 462 -
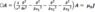 upload_2017-11-19_23-5-23.png1,018 bytes · Views: 445
upload_2017-11-19_23-5-23.png1,018 bytes · Views: 445 -
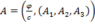 upload_2017-11-19_23-6-41.png660 bytes · Views: 431
upload_2017-11-19_23-6-41.png660 bytes · Views: 431 -
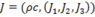 upload_2017-11-19_23-7-31.png553 bytes · Views: 419
upload_2017-11-19_23-7-31.png553 bytes · Views: 419