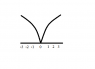
maplesyrup23
- 10
- 0
I'm trying to find the limit of this function at 0.
I know that for the abs (x) graph, 0 is not differentiable because of abs (h)/h, but I'm not certain about the point on this function.
There is no function given, only the picture.
Thanks in advance!
I know that for the abs (x) graph, 0 is not differentiable because of abs (h)/h, but I'm not certain about the point on this function.
There is no function given, only the picture.
Thanks in advance!