Limit of Cosine Function without Taylor Series

[Char. Limit]

Homework Statement

So, I was reviewing limits for some reason, and I came across one that couldn't be solved:

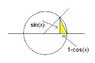
$$\stackrel{lim}{x\rightarrow0} \frac{cos(x)-1}{x^2}$$

Homework Equations

Are there any? I'm not sure.

The Attempt at a Solution

Now, I could do this limit easily if I had the Taylor series for cosine at my disposal (using that method, I got -1/2), but I'm trying to do this limit without using the derivative of the cosine, which essentially means Taylor series is out. And considering that limits were sort of just glanced over in my Calc I class, not really delved into, how would I solve this without assuming a derivative for the cosine?

 

[Dick]

If you are living in a world without derivatives, then you'll have to try and use a geometric argument. Draw a unit circle and a right triangle with central angle x, one leg along the x-axis. Use that when x is small the hypotenuse is approximately equal to the arc length. I.e. the hypotenuse is ~x. Do you see the picture? Now use Pythagoras.

 

[Char. Limit]

I'm afraid I don't see it... you say the central angle is x, but then later you say that the hypotenuse is ~x because it's close to the arc length (of which arc?). Which is it, or is it both?

 

[ehild]

You can use the identity 1-cos(x)=2sin²(x/2), and then using the limit (sinx/x) =1 when x-->0

ehild

 

[Dick]

Ack. I should learn to make pictures sometime. The central angle is x (in RADIANS). So the length of the arc subtended by x on a unit circle is x. Since arclength=r*angle. And r is 1. That's very closely equal the chord of the subtended arc with central angle x when x is small. Do you see that? If you wait for me to draw a picture, it might take a few days.

 

[Dick]

Do you know l'Hôpital's rule?

ehild

Of course Char. Limit does. I think the ground rules here are to do this without using derivatives. If you can help to explain the geometric argument that would be great.

 

[Char. Limit]

Ack. I should learn to make pictures sometime. The central angle is x (in RADIANS). So the length of the arc subtended by x on a unit circle is x. Since arclength=r*angle. And r is 1. That's very closely equal the chord of the subtended arc with central angle x when x is small. Do you see that? If you wait for me to draw a picture, it might take a few days.

Oh, the chord! I thought you meant the arc length approached the hypotenuse length.

 

[ehild]

Rewrite the limit in terms of sin(x/2)/(x/2)and use that it is 1 when x tends to 0. This limit is obtained from the figure attached:
sin(x)<x<tan(x) (x is the arc which can be approximated with the cord) and dividing the inequality by sin(x)ehild

 

[Char. Limit]

Well, so far three methods (Taylor Series, L'Hopital's rule, and Ehild's Substitution), and they all gave me -1/2, but for some reason the geometric version gave me -1. I drew the unit circle, a triangle with central angle x, and noticed that as x-->0, the chord was ~x, and the adjacent side was ~1. This made the hypotenuse ~1+x^2, and the cosine of x ~1/(1+x^2). So I substituted that in for cos(x).

$$\frac{\frac{1}{1+x^2} - 1}{x^2}$$

$$\frac{\frac{1}{1+x^2}-\frac{1+x^2}{1+x^2}}{x^2}$$

$$\frac{\frac{1-1-x^2}{1+x^2}}{x^2}$$

$$-\frac{\frac{x^2}{1+x^2}}{x^2}$$

$$-\frac{x^2}{x^2(1+x^2)}$$
$$-\frac{1}{1+x^2}$$

Which tends to -1 as x tends to 0.

 

[Dick]

Oh, the chord! I thought you meant the arc length approached the hypotenuse length.

Actually, that is what I meant. The chord and the arc are approximately equal. So if you've drawn the right triangle you should be looking at sin(x)^2+(1-cos(x))^2~x^2. I'm not sure how rigorous that is but that's how I seem to remember the argument.

 

[ehild]

Well, so far three methods (Taylor Series, L'Hopital's rule, and Ehild's Substitution), and they all gave me -1/2, but for some reason the geometric version gave me -1.

I can not follow you without picture.
See my one. Calculate the length of chord from the yellow triangle.

ehild

 

[Dick]

I can not follow you without picture.
See my one. Calculate the length of chord from the yellow triangle.

ehild

Thank you for the picture, ehild. That's just what I needed. And the sin(x)<x<tan(x) is probably what you need to actually make it rigorous.

 

[Char. Limit]

Wow, I completely misunderstood Dick's description. So, with this new picture, I get that...

$$sin^2(x)+\left(1-cos(x)\right)^2\approx x^2$$

$$sin^2(x) + 1 - 2 cos(x) + cos^2(x) \approx x^2$$

$$2-2cos(x) = 2(1-cos(x)) \approx x^2$$

$$1-cos(x) \approx \frac{x^2}{2}$$

For very small x. Correct? So, putting that in...

$$lim_{x\rightarrow0}{x\frac{cos(x)-1}{x^2} = lim_{x\rightarrow0}-\frac{1-cos(x)}{x^2}$$

$$=lim_{x\rightarrow0}-\frac{\frac{x^2}{2}}{x^2}$$

$$=lim_{x\rightarrow0}-\frac{x^2}{2x^2}=lim_{x\rightarrow0}-\frac{1}{2}=-\frac{1}{2}$$

Thus concludes the proof?

 

[Bohrok]

Wouldn't it be easier to multiply by (cosx + 1)/(cosx + 1) and use the limit for sinx/x?

 

[ehild]

Char, it is more or less OK. So you start out from chord/arc-->1 for x--->0
You know that arc=x. Determine the length of chord from the triangle:

chord²=2(1-cosx),

2(1-cosx)/x² --->1

-(1-cosx)/x²-->-1/2

ehild