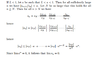- #1
MstrGnrl
- 3
- 0
Hello Folks,
I am solving a limit proof that has the following attached solution.
Question: Assume all sn ≠ 0. and that the limit L = lim abs(sn+1/sn) exists. Show that if L<1. the lim sn=0
I Understand the solution except for one part which is also attached..
sn = sN*sN+1/sN*** sn/sn-1
Can someone please explain this portion of the problem? I don't understand how sN+2 cancels with sn-1.. It definitely has something to do with n≥N but how they derived it I am not sure
Thanks
I am solving a limit proof that has the following attached solution.
Question: Assume all sn ≠ 0. and that the limit L = lim abs(sn+1/sn) exists. Show that if L<1. the lim sn=0
I Understand the solution except for one part which is also attached..
sn = sN*sN+1/sN*** sn/sn-1
Can someone please explain this portion of the problem? I don't understand how sN+2 cancels with sn-1.. It definitely has something to do with n≥N but how they derived it I am not sure
Thanks
Attachments
Last edited: