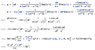A Limits of the classical oscillator

[itssilva]

Some time ago I was playing with the oscillator when I noticed a few funny things. Consider first the 1D oscillator with Hamiltonian $$ \displaystyle H(q,p) = \frac{p^2}{2m} + \frac{m\omega^2}{2}q^2$$ whose solutions are $$ q(t) = q_0cos(\omega t) + \frac{p_0}{m\omega}sin(\omega t), p(t) = m \dot q(t); $$ Also, since the Hamiltonian is time-independent, the energy is a constant of motion given by $$ \displaystyle E(q_0,p_0) = \frac{p_0^2}{2m} + \frac{m\omega^2}{2}q_0^2$$ Now, perhaps unsurprisingly, I notice that taking $\omega \rightarrow 0$ as $O(\omega^2) \sim 0$ will reduce this problem to that of the free 1D particle. Okay. But now consider the driven oscillator with Hamiltonian $$ \displaystyle H(q,p,t) = \frac{p^2}{2m} + \frac{m\omega^2}{2}q^2 + \lambda cos(\omega_d t)q $$ with solutions $$ q(t) = q_0cos(\omega t) + \frac{p_0}{m\omega}sin(\omega t) + \frac{\lambda}{m(\omega_d^2 - \omega^2)}cos(\omega_d t), p(t) = m \dot q(t); $$ Now the energy is given by $$ \displaystyle E(q_0,p_0,t) = \frac{p_0^2}{2m} + \frac{m\omega^2}{2}q_0^2 + \omega q_0p_0sin(2\omega t) + O(\lambda) $$ (done by hand+Wolfram Alpha - but you may want to double-check it); so, it appears that the previous "trick" doesn't quite work here as well (note that $O(\lambda)$ is linear in $q_0,p_0)$. So 1) I wonder if this is a true "anomaly", and 2) whether there are other known examples (classical or quantum, as may be appropriate here; I was studying the quantum problem when I noticed this detail).

(P.S.: Finally I get myself to post here in LaTex; I'm beaming )

 

[kuruman]

By "trick" do you mean reducing the Hamiltonian to that of a free particle in the limit $\omega \rightarrow 0$? Maybe I'm missing your point, but don't you have to do something about the driving force as well? Is the particle expected to be "free" when it's acted upon by a driving force?

 

[itssilva]

By "trick" do you mean reducing the Hamiltonian to that of a free particle in the limit $\omega \rightarrow 0$? Maybe I'm missing your point, but don't you have to do something about the driving force as well? Is the particle expected to be "free" when it's acted upon by a driving force?

I mean as in a hierarchy: a harmonic oscillator goes to a free particle as the natural frequency $\omega$ gets arbitrarily small (checks with intuition), but the driven oscillator doesn't go to the harmonic one as either the amplitude $\lambda$ or the driving frequency $\omega_d$ vanish (doesn't check with intuition); so imagine the empirical ambiguity, as you have a driven oscillator with $\lambda$ or $\omega_d$ as control parameters, which you can smoothly lower to your heart's desire. That's why I think there's a pathology or mistake here.

 

[Orodruin]

You should certainly not expect to recover a free particle in the limit where the driving frequency goes to zero. That limit is just the limit of a particle in a linear potential.

In the limit $\lambda \to 0$ your solution goes back to the harmonic oscillator solution to zeroth order in $\lambda$.

 

[itssilva]

You should certainly not expect to recover a free particle in the limit where the driving frequency goes to zero

Well yeah, but what I said was that you get a free particle as the natural frequency of the harmonic osc. goes to zero; as for

In the limit $\lambda \to 0$ your solution goes back to the harmonic oscillator solution to zeroth order in $\lambda$.

I don't get it - as you can see from the expression of the energy $\displaystyle E(q_0,p_0,t)$, it doesn't go to that of the harmonic osc. in that limit; if you mean there's an error in the calculation (which I suspect as much), would you mind showing your own?

 

[kuruman]

Since you have done the derivation of $E(q_0,p_0,t)$ by hand and by Wolfram, can you explain why the expression for it is independent of $\omega_d$? Or is the term $\sin(2\omega t)$ a typo?

 

[Orodruin]

Well yeah, but what I said was that you get a free particle as the natural frequency of the harmonic osc. goes to zero;

This is not true either. A particle under the influence of an external driving force is not free.

I don't get it - as you can see from the expression of the energy $\displaystyle E(q_0,p_0,t)$, it doesn't go to that of the harmonic osc. in that limit; if you mean there's an error in the calculation (which I suspect as much), would you mind showing your own?

It would seem to me that your expression for the energy cannot be correct. All terms that are not proportional to at least one power of $\lambda$ are just the regular solution to the harmonic oscillator. Please show how you got there.

Edit: It occurs to me that you are likely missing a minus sign in the derivative $\dot q$. This would mean that the cross term between the momentum and displacement initial conditions would not cancel and instead you would get something like the term you quote.

 

[itssilva]

This is not true either. A particle under the influence of an external driving force is not free.

I believe you're attacking a strawman there: I referred to the first part of my post - the one that does not introduce a driving force; if you have trouble seeing it, just expand $H, q, E$ in powers of $\omega$ and kill off those terms higher than first-order: you will get the free particle, which makes sense: a free particle is identical to a harmonic osc. with $\omega = 0$.

Edit: It occurs to me that you are likely missing a minus sign in the derivative $\dot q$

After Hamilton: $$ \dot q = \frac {\partial H} {\partial p}, - \dot p = \frac {\partial H} {\partial q}; $$however, I did make a typo in the OP: instead of $q_0$ in the solution for the driven osc., substitute $q_0 - \frac{\lambda}{m(\omega_d^2 - \omega^2)}$ (if you're taking, as me, $q_0 = q(0), p_0 = p(0)$).

I'm sending the full expression of the energy I obtained in a .pdf file; you may conflate it with that of other CAS's, as well.

 

[Orodruin]

You are doing something wrong when you are inserting the solution into the Hamiltonian. This should be clear from the fact that any term in your expressions that has to do with the driving force is proportional to at least one order of lambda. This is my Mathematica output of the insertion you should be making: